如图所示,C是放在光滑的水平面上的一块木板,木板的质量为3m,在木板的上面有两块质量均为m的小木块A和B,它们与木板间的动摩擦因数均为μ。最初木板静止,A、B两木块同时以方向水平向右的初速度v0和2v0在木板上滑动,木板足够长,A、B始终未滑离木板。求:
(1)木块B从刚开始运动到与木板C速度刚好相等的过程中,木块B所发生的位移;
(2)木块A在整个过程中的最小速度。
如图13-1-9所示,水面上漂浮着一半径为r的圆形薄木板,在木板圆心的正上方距木板高度h的A处有一个点光源S.由于木板的影响,点光源发出的光线射入水中后,在水底平面上形成一圆形阴影.已知水深为H,水的折射率为n,求阴影的半径.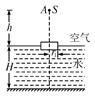
图13-1-9
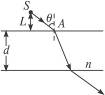
在折射率为n、厚度为d的玻璃平板上方的空气中有一点光源S,从S发出的光线SA以入射角θ入射到玻璃板上表面,经过玻璃板后从下表面射出,如图19-2-13所示.若沿此光线传播的光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等,点光源S到玻璃板上表面的垂直距离l应是多少?
如图19-2-9所示,一束平行光以30°的入射角从玻璃射向空气中,折射角为45°,求:
(1)玻璃的折射率;
(2)光在玻璃中的传播速度.
图19-2-9
一半圆形玻璃砖,玻璃的折射率为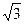 ,AB为其直径,长度为D,O为圆心.一束宽度恰等于玻璃砖半径的单色平行光束垂直于AB从空气射入玻璃砖,其中心光线P通过O点,如图19-2-17所示.M、N为光束边界光线.则M、N射出玻璃砖后的相交点距O点的距离为多少?
,AB为其直径,长度为D,O为圆心.一束宽度恰等于玻璃砖半径的单色平行光束垂直于AB从空气射入玻璃砖,其中心光线P通过O点,如图19-2-17所示.M、N为光束边界光线.则M、N射出玻璃砖后的相交点距O点的距离为多少?
图19-2-17
在折射率为n、厚度为d的玻璃平板上方的空气中有一点光源S,从S发出的光线SA以角度θ入射到玻璃板上表面,经过玻璃板后从下表面射出,如下图所示.若沿此光线传播的光从光源到玻璃板上表面的传播时间与在玻璃板中的传播时间相等,点光源S到玻璃板上表面的垂直距离L应是多少?