如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点。(1)若平面ABCD ⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME 与 BN 是两条异面直线

已知向量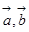 满足
满足 ,且
,且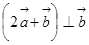 .
.
(1)、求向量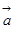 的坐标;(2)、求向量
的坐标;(2)、求向量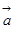 与
与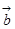 的夹角.
的夹角.
已知圆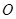 的方程为
的方程为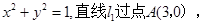 且与圆
且与圆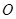 相切.
相切.
(1)求直线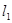 的方程;
的方程;
(2)设圆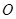 与
与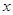 轴交于
轴交于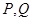 两点,M是圆
两点,M是圆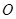 上异于
上异于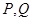 的任意一点,过点
的任意一点,过点 且与
且与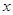 轴垂直的直线为
轴垂直的直线为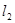 ,直线
,直线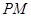 交直线
交直线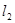 于点P’,直线
于点P’,直线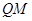 交直线
交直线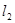 于点Q’
于点Q’
求证:以P’Q’为直径的圆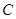 总过定点,并求出定点坐标.
总过定点,并求出定点坐标.
已知函数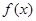 在
在 上是增函数,若不等式
上是增函数,若不等式 对于任意
对于任意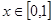 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为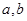 .
.
(1)求直线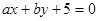 与圆
与圆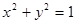 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
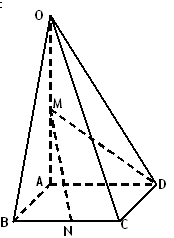
如图,在四棱锥O—ABCD中,底面ABCD是边长为1的菱形,∠ABC=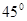 ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点。
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点。
(1)证明:直线MN∥平面OCD;
(2)求异面直线AB与MD所成角的大小;