已知圆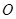 的方程为
的方程为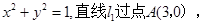 且与圆
且与圆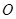 相切.
相切.
(1)求直线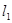 的方程;
的方程;
(2)设圆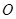 与
与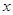 轴交于
轴交于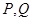 两点,M是圆
两点,M是圆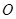 上异于
上异于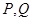 的任意一点,过点
的任意一点,过点 且与
且与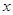 轴垂直的直线为
轴垂直的直线为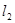 ,直线
,直线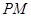 交直线
交直线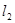 于点P’,直线
于点P’,直线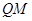 交直线
交直线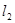 于点Q’
于点Q’
求证:以P’Q’为直径的圆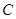 总过定点,并求出定点坐标.
总过定点,并求出定点坐标.
(本小题满分14分)在平面直角坐标系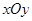 中,
中,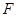 是抛物线
是抛物线
 的焦点,
的焦点,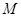 是抛物线
是抛物线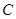 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过 三点的圆的圆心为
三点的圆的圆心为 ,点
,点 到抛物线
到抛物线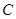 的准线的距离为
的准线的距离为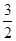 .(Ⅰ)求抛物线
.(Ⅰ)求抛物线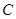 的方程;(Ⅱ)是否存在点
的方程;(Ⅱ)是否存在点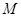 ,使得直线
,使得直线 与抛物线
与抛物线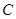 相切于点
相切于点 若存在,求出点
若存在,求出点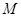 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
如图,在矩形ABCD中,AB=2BC,点M在边CD上,点F在边AB上,且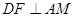 ,垂足为E,若将
,垂足为E,若将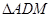 沿AM折起,使点D位于
沿AM折起,使点D位于 位置,连接
位置,连接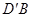 ,
,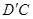 得四棱锥
得四棱锥 .
.
(1)求证: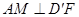 ;(2)若
;(2)若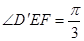 ,直线
,直线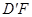 与平面ABCM所成角的大小为
与平面ABCM所成角的大小为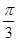 ,求直线
,求直线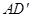 与平面ABCM所成角的正弦值.
与平面ABCM所成角的正弦值.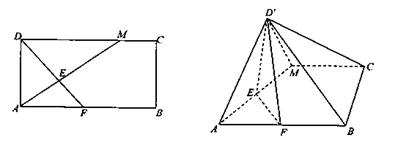
(本题14分)设数列 是首项为
是首项为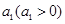 ,公差为
,公差为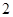 的等差数列,其前
的等差数列,其前 项和为
项和为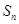 ,且
,且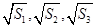 成等差数列.
成等差数列.
(Ⅰ)求数列 的通项公式;(Ⅱ)记
的通项公式;(Ⅱ)记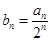 的前
的前 项和为
项和为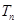 ,求
,求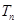 .
.
(本题14分)向量 ,设函数
,设函数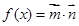 .
.
(1)求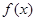 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在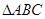 中,
中,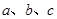 分别是角
分别是角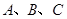 的对边,若
的对边,若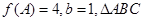 的面积
的面积
为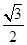 ,求a的值.
,求a的值.
(本题满分15分 )已知函数 .
.
(1)求函数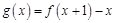 的最大值;
的最大值;
(2)若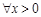 ,不等式
,不等式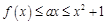 恒成立,求实数
恒成立,求实数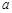 的取值范围;
的取值范围;
(3)若 ,求证:
,求证: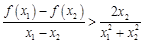 .
.