社区文具商场的某种毛笔每支售价25元,书法练习本每本售价5元.该商场为促销制定了甲、乙两种优惠方案:方案甲:买1支毛笔就赠送1本书法练习本;方案乙:按购买金额打9折付款.某校书法兴趣小组打算购买这种毛笔10支,这种书法练习本 (
( )本.
)本.
(1)分别写出按甲、乙两种优惠方案实际付款金额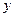 甲(元)、
甲(元)、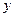 乙(元)与
乙(元)与 之间的函数关系式;
之间的函数关系式;
(2)如果该商场即允许只选择一种优惠方案购买,也允许同时用两种优惠方案购买,请你就购买这种毛笔10支和这种书法练习本60本设计一种最省钱的购买方案.
(本小题满分12分)已知函数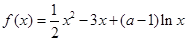 ,
, ,
,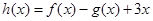 ,其中
,其中 且
且 .
.
(I)求函数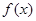 的导函数
的导函数 的最小值;
的最小值;
(II)当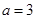 时,求函数
时,求函数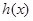 的单调区间及极值;
的单调区间及极值;
(III)若对任意的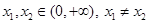 ,函数
,函数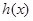 满足
满足 ,求实数
,求实数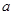 的取值范围.
的取值范围.
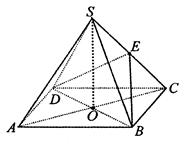
如图,四棱锥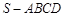 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形, 是
是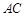 与
与 的交点,
的交点,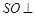 平面
平面 ,
,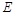 是侧棱
是侧棱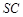 的中点,异面直线
的中点,异面直线 和
和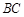 所成角的大小是60
所成角的大小是60 .
.
(Ⅰ)求证:直线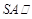 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)已知函数 (
( ),直线
),直线 ,
, 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且 的最小值为
的最小值为 .
.
(I)求 的表达式;
的表达式;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数 的图象,若关于
的图象,若关于 的方程
的方程 ,在区间
,在区间 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知各项都不相等的等差数列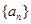 的前6项和为60,且
的前6项和为60,且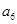 为
为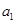 和
和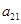 的等比中项.
的等比中项.
( I )求数列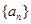 的通项公式;
的通项公式;
(II) 若数列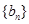 满足
满足 ,且
,且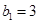 ,求数列
,求数列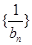 的前
的前 项和
项和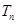 .
.
(本小题满分12分)已知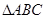 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,设向量
,设向量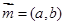 ,
,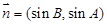 ,
, 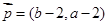
(Ⅰ)若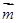 ∥
∥ ,求证:
,求证: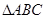 为等腰三角形;
为等腰三角形;
(Ⅱ)若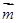 ⊥
⊥ ,边长
,边长 ,
, ,求
,求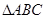 的面积.
的面积.