(本小题满分12分)已知函数 (
( ),直线
),直线 ,
, 是
是 图象的任意两条对称轴,且
图象的任意两条对称轴,且 的最小值为
的最小值为 .
.
(I)求 的表达式;
的表达式;
(Ⅱ)将函数 的图象向右平移
的图象向右平移 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数 的图象,若关于
的图象,若关于 的方程
的方程 ,在区间
,在区间 上有且只有一个实数解,求实数
上有且只有一个实数解,求实数 的取值范围.
的取值范围.
(本题满分13分)
某学校数学兴趣小组有10名学生,其中有4名女同学;英语兴趣小组有5名学生,其中有3名女学生,现采用分层抽样方法(层内采用不放回简单随机抽样)从数学兴趣小组、英语兴趣小组中共抽取3名学生参加科技节活动。
(1)求从数学兴趣小组、英语兴趣小组各抽取的人数;
(2)求从数学兴趣小组抽取的学生中恰有1名女学生的概率;
(3)记 表示抽取的3名学生中男学生数,求
表示抽取的3名学生中男学生数,求 的分布列及数学期望。
的分布列及数学期望。
已知数列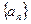 中,
中,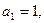 且点
且点 在直线
在直线 上.
上.
(1)求数列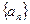 的通项公式;
的通项公式;
(2)若函数
求函数 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前
的前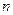 项和.试问:是否存在关于
项和.试问:是否存在关于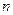 的整式
的整式 ,使得
,使得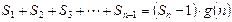 对于一切不小于2的自然数
对于一切不小于2的自然数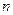 恒成立? 若存在,写出
恒成立? 若存在,写出 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
设斜率为 的直线
的直线 交椭圆
交椭圆 :
: 于
于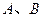 两点,点
两点,点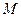 为弦
为弦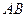 的中点,直线
的中点,直线 的斜率为
的斜率为 (其中
(其中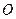 为坐标原点,假设
为坐标原点,假设 、
、 都存在).
都存在).
(1)求 ×
× 的值.
的值.
(2)把上述椭圆 一般化为
一般化为 (
(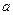 >
> >0),其它条件不变,试猜想
>0),其它条件不变,试猜想 与
与 关系(不需要证明).请你给出在双曲线
关系(不需要证明).请你给出在双曲线 (
(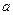 >0,
>0, >0)中相类似的结论,并证明你的结论.
>0)中相类似的结论,并证明你的结论.
有一种变压器铁芯的截面呈正十字形,为保证所需的磁通量,要求正十字形的面积为4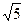 cm2,为了使用来绕铁芯的铜线最省,即正十字形外接圆周长最短,应如何设计 正十字形的长和宽?
cm2,为了使用来绕铁芯的铜线最省,即正十字形外接圆周长最短,应如何设计 正十字形的长和宽?
已知函数 是奇函数.
是奇函数.
(1)求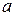 的值;
的值;
(2)判断函数 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)求函数的值域.