质量为5×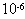 kg的带电粒子以
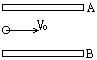
kg的带电粒子以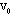 =2m/s的速度从水平放置的平行金属板A、B中央水平飞入板间,如图示,已知板长L=10cm,板间距离d=2cm,当
=2m/s的速度从水平放置的平行金属板A、B中央水平飞入板间,如图示,已知板长L=10cm,板间距离d=2cm,当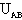 =1000V时,带电粒子恰好沿直线穿过板间,问粒子所带电荷的符号及量值,并计算AB间电压在什么范围内带电粒子能从板间飞出(g取10m/
=1000V时,带电粒子恰好沿直线穿过板间,问粒子所带电荷的符号及量值,并计算AB间电压在什么范围内带电粒子能从板间飞出(g取10m/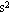 )
)
[物理--选修3-3]
(1)氧气分子在 和 温度下单位速率间隔的分子数占总分子数的百分比随气体分子速率的变化分别如图中两条曲线所示.下列说法正确的是( )

| A. |
图中两条曲线下面积相等 |
| B. |
图中虚线对应于氧气分子平均动能较小的情形 |
| C. |
图中实线对应于氧气分子在 时的情形 |
| D. |
图中曲线给出了任意速率区间的氧气分子数目 |
| E. |
与0℃时相比,100℃时氧气分子速率出现在 区间内的分子数占总分子数的百分比较大 |
(2)如图,容积均为V的汽缸A、B下端有细管(容积可忽略)连通,阀门 位于细管的中部,A、B的顶部各有一阀门 、 ,B中有一可自由滑动的活塞(质量、体积均可忽略).初始时,三个阀门均打开,活塞在B的底部;关闭 、 ,通过 给汽缸充气,使A中气体的压强达到大气压p 0的3倍后关闭 .已知室温为27℃,汽缸导热.
(i)打开 ,求稳定时活塞上方气体的体积和压强;
(ii)接着打开 ,求稳定时活塞的位置;
(iii)再缓慢加热汽缸内气体使其温度升高20℃,求此时活塞下方气体的压强.

真空中存在电场强度大小为 的匀强电场,一带电油滴在该电场中竖直向上做匀速直线运动,速度大小为 ,在油滴处于位置A时,将电场强度的大小突然增大到某值,但保持其方向不变.持续一段时间 后,又突然将电场反向,但保持其大小不变;再持续同样一段时间后,油滴运动到B点.重力加速度大小为g.
(1)油滴运动到B点时的速度;
(2)求增大后的电场强度的大小;为保证后来的电场强度比原来的大,试给出相应的 和 应满足的条件.已知不存在电场时,油滴以初速度v 0做竖直上抛运动的最大高度恰好等于B、A两点间距离的两倍.
(1)一静止的铝原子核 俘获一速度为 的质子p后,变为处于激发态的硅原子核 ,下列说法正确的是_________
| A. |
核反应方程为 |
| B. |
核反应方程过程中系统动量守恒 |
| C. |
核反应过程中系统能量不守恒 |
| D. |
核反应前后核子数相等,所以生成物的质量等于反应物的质量之和 |
| E. |
硅原子核速度的数量级为 ,方向与质子初速度方向一致 |
(2)如图所示,水平地面上有两个静止的小物块a和b,其连线与墙垂直:a和b相距l;b与墙之间也相距l;a的质量为m,b的质量为 ,两物块与地面间的动摩擦因数均相同,现使a以初速度 向右滑动,此后a与b发生弹性碰撞,但b没有与墙发生碰撞,重力加速度大小为g,求物块与地面间的动摩擦力因数满足的条件。

(1)由波源S形成的简谐横波在均匀介质中向左、右传播。波源振动的频率为20 Hz,波速为16 m/s。已知介质中P、Q两质点位于波源S的两侧,且P、Q和S的平衡位置在一条直线上,P、Q的平衡位置到S的平衡位置之间的距离分别为15.8 m、14.6 m,P、Q开始震动后,下列判断正确的是_____。
| A. |
P、Q两质点运动的方向始终相同 |
| B. |
P、Q两质点运动的方向始终相反 |
| C. |
当S恰好通过平衡位置时,P、Q两点也正好通过平衡位置 |
| D. |
当S恰好通过平衡位置向上运动时,P在波峰 |
| E. |
当S恰好通过平衡位置向下运动时,Q在波峰 |
(2)如图,玻璃球冠的折射率为 ,其底面镀银,底面的半径是球半径的 倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点。求该光线从球面射出的方向相对于其初始入射方向的偏角。

在“探究求合力的方法”的实验中,实验方案如下图所示
(1)下列措施中,为了保证力的作用效果相同的措施是()
| A.每次将橡皮条拉到同样的位置 |
| B.每次把橡皮条拉直 |
| C.每次准确读出弹簧秤的示数 |
| D.每次记准细绳方向 |
(2)结合图1和图2中的钩码数量,可判断 。
。
(3)若把支柱B水平向右稍微偏移,而不改变左侧的钩码数量,同时把支柱C稍微向左偏移,那么左侧钩码的数量该如何改变?