如图所示的装置中，N为水平放置的金属网板，M为与之平行的金属板，MN相距4.5cm，两板间电压
=2.30V，网板上方为垂直纸面大小为6.28×
T的匀强磁场，P与S正对．设想在某一时刻，一个自由电子从P点由静止开始运动，并穿过网板最后到达S'，已知SS'相距3.27×
m，设自由电子始终不会被吸附，整个装置放在真空中．求该自由电子从P第一次到达S'所需的时间．(电子荷质比e/m=1.76×
C/kg)
地球围绕太阳的运动可以视为匀速圆周运动，若地球距太阳的距离为 r，地球绕太阳公转周期为 T，若已知万有引力常量为 G，那么太阳的质量是多少？
在如图所示的十字路口处，有一辆长9m、宽2.1m的客车，客车正以10m/s速度正常匀速行驶在马路中间，当它与斑马线的中点B相距62m时，马路边上的小王同学正好在斑马线中间A点出发沿AB穿过马路，A、B间的距离为8m，问:小王同学运动的速度为多大时，能够安全过马路?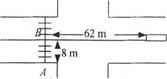
一辆质量为4 t的汽车驶过半径为50 m的凸形桥面时，始终保持5 m/s的速率.汽车所受的阻力为车与桥面压力的0.05倍.通过桥的最高点时汽车牵引力是多少？(g="10" m/s2)
如图所示，用同种材料制成一个竖直平面内的轨道，AB段为
圆弧，半径为R，BC段水平且长度为R，一小物块质量为m与轨道间动摩擦因数为
．当它从轨道顶端A无初速下滑时，恰好运动到C点静止，求：
（1）物体在AB段克服摩擦力做的功．
（2）若选A点所在的水平面为零势能面，物体到达B点时的机械能．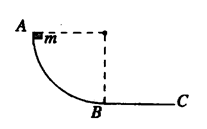
如图所示，光滑斜面的倾角为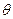
，高为h，有一质量为m的物体从斜面顶端由静止开始滑到底端，求：
（1）物体在整个下滑过程中重力做功的平均功率；
（2）物体滑到底端时重力做功的瞬时功率．