某企业准备投产一种新产品，经测算，已知每年生产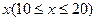
万件的该种产品所需要的总成本为
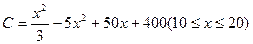万元，市场销售情况可能出现好、中、差三种情况，各种情况发生的概率和相应的价格p（元）与年产量x之间的函数关系如下表所示.
| 市场情况 |
概率 |
价格p与产量x的函数关系式 |
| 好 |
0.3 |
 |
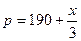| 中 |
0.5 |
 |
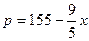| 差 |
0.2 |
 |
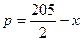设L1、L2、L3分别表示市场情况好、中、差时的利润，随机变量ξx表示当年产量为x而市场情况不确定时的利润.
（1）分别求利润L1、L2、L3与年产量x之间的函数关系式；
（2）当产量x确定时，求随机变量ξx的期望Eξx；
（3）求年产量x为何值时，随机变量ξx的期望Eξx取得最大值（不需求最大值）.
某观测站C在A城的南偏西20°的方向.由A城出发的一条公路，走向是南偏东40°，在C处测得公路上B处有一人距C为31千米正沿公路向A城走去，走了20千米后到达D处，此时CD间的距离为21千米，问这人还要走多少千米才能到达A城？
如图所示，已知半圆的直径AB=2，点C在AB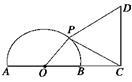
的延长线上，BC=1，点P为半圆上的一个动点，以
DC为边作等边△PCD，且点D与圆心O分别在PC
的两侧，求四边形OPDC面积的最大值.
沿一条小路前进，从A到B，方位角（从正北方向顺时针转到AB方向所成的角）是
50°，距离是3 km，从B到C，方位角是110°，距离是3 km，从C到D,方位角是140°，距离是（9+3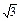
）km.试画出示意图，并计算出从A到D的方位角和距离（结果保留根号）.
要测量对岸A、B两点之间的距离，选取相距
km的C、D两点，并测得∠ACB=75°，∠BCD=45°，∠ADC=30°，∠ADB=45°，求A、B之间的距离.
在△ABC中，角A、B、C的对边分别为a、b、c，已知a+b=5，c=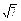
，且4sin2
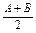-cos2C=
.
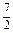(1)求角C的大小；
（2）求△ABC的面积.