在平面直角坐标系xOy中,已知椭圆C:
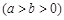 的离心率为
的离心率为 ,且过点
,且过点 ,过椭圆的左顶点A作直线
,过椭圆的左顶点A作直线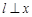 轴,点M为直线
轴,点M为直线 上的动点,点B为椭圆右顶点,直线BM交椭圆C于P.
上的动点,点B为椭圆右顶点,直线BM交椭圆C于P.
(1)求椭圆C的方程;
(2)求证: ;
;
(3)试问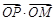 是否为定值?若是定值,请求出该定值;若不是定值,请说明理由.
是否为定值?若是定值,请求出该定值;若不是定值,请说明理由.
设正有理数 是
是 的一个近似值,令
的一个近似值,令 .
.
(1) 若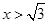 ,求证:
,求证: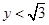 ;
;
(2) 求证: 比
比 更接近于
更接近于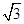 .
.
设函数 .
.
(1)解不等式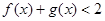 ;
;
(2)对于实数 ,若
,若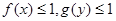 ,求证
,求证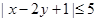 .
.
如图,建立平面直角坐标系 ,
, 轴在地平面上,
轴在地平面上, 轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程
轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程 表示的曲线上,其中
表示的曲线上,其中 与发射方向有关.炮的射程是指炮弹落地点的横坐标.
与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1) 求炮的最大射程;
(2) 设在第一象限有一飞行物(忽略其大小),其飞行高度为 千米,试问它的横坐标
千米,试问它的横坐标 不超过多少时,炮弹可以击中它?请说明理由.
不超过多少时,炮弹可以击中它?请说明理由.
已知函数
 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3)
的图像经过点(1,3)
(1)求实数 的值;
的值;
(2)求函数 的值域.
的值域.
设函数
(1) 设 ,
, ,当
,当 时,求
时,求 的单调区间和值域;
的单调区间和值域;
(2)设 为偶数时,
为偶数时, ,
, ,求
,求 的最小值和最大值.
的最小值和最大值.