
一个空间几何体 的三视图如图所 示,其中
的三视图如图所 示,其中 分别是
分别是 五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形
五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形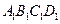 为正方形且
为正方形且 ;在左视图中
;在左视图中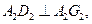 俯视图中
俯视图中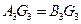 ,
,
(Ⅰ)根据三视图作出空间几何体 的直观图,并标明
的直观图,并标明 五点的位置;
五点的位置;
(Ⅱ)在空间几何体 中,过点
中,过点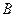 作平面
作平面 的垂线,若垂足H在直线
的垂线,若垂足H在直线 上,求证:平面
上,求证:平面 ⊥平面
⊥平面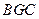 ;
;
(Ⅲ)在(Ⅱ)的条件下,求三棱锥 的体积及其外接球的表面积.
的体积及其外接球的表面积.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 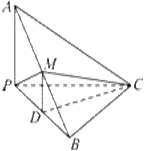
(1)求证DM∥平面APC;
(2)求证平面ABC⊥平面APC;
(3)若BC=PC=4,求二面角P-AB-C的正弦值.
已知数列 是一个等差数列且
是一个等差数列且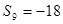 ,
, ,
,
(1)求 通项公式;
通项公式;
(2)求 的前
的前 项和
项和 的最小值.
的最小值.
风景秀美的湖畔有四棵高大的银杏树,记做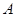 、
、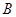 、
、 、
、 ,欲测量
,欲测量 、
、 两棵树和
两棵树和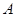 、
、 两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得
两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得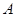 、
、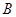 两点间的距离为
两点间的距离为 米,如图,同时也能测量出
米,如图,同时也能测量出 ,
,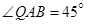 ,
, ,
, ,则
,则 、
、 两棵树和
两棵树和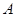 、
、 两棵树之间的距离各为多少?
两棵树之间的距离各为多少?
(本小题满分8分)在 中,a,b,c分别是内角A,B,C所对的边,
中,a,b,c分别是内角A,B,C所对的边, .
.
(1)求角C;
(2)若 ,
, ,求
,求 的面积.
的面积.
在直角坐标系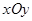 中,以
中,以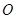 为圆心的圆与直线
为圆心的圆与直线 相切,求圆
相切,求圆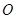 的方程.
的方程.