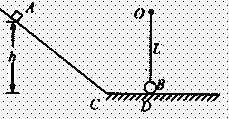
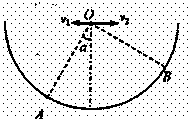
如图所示，用同种材料制成一个竖直平面内的轨道，AB段为
圆弧，半径为R，BC段水平且长度为R，一小物块质量为m与轨道间动摩擦因数为
．当它从轨道顶端A无初速下滑时，恰好运动到C点静止，求：
（1）物体在AB段克服摩擦力做的功．
（2）若选A点所在的水平面为零势能面，物体到达B点时的机械能．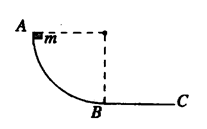
如图所示，电阻不计的平行金属导轨MN和OP放置在水平面内，MO间接有阻值为R=3Ω的电阻。导轨相距d=1m，其间有竖直向下的匀强磁场，磁感强度B=0.5T。质量为m=0.1kg，电阻为r=lΩ的导体棒CD垂直于导轨放置，并接触良好。用平行于MN向右的恒力F=1N向右拉动CD，CD受摩擦阻力f恒为0.5N。求：
（1）CD运动的最大速度是多少?
（2）当CD达到最大速度后，电阻R消耗的电功率是多少?
（3）当CD的速度为最大速度的一半时，CD的加速度是多少?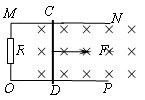
（1）请举出日常生活中你观察到的一个关于多普勒效应的实例．
．
（2）图示为一列简谐横波在某时刻的波形图，已知图中 B 质点起振比A 质点早0.2s，B 和 C 之间的距离是0.3m，则此列波沿传播，波速为m/s．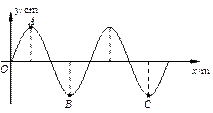
（3）某同学在家里做用单摆测定重力加速度的实验，由于没有螺旋测微器测摆球的直径，采用了如下方法：先用秒表测得单摆周期为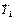
，然后让悬线缩短
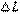，再次测得单摆周期为
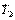，那么该同学测得的重力加速度为多少？
（1）4s末物体速度的大小；
|
（2）在图丙的坐标系中画出物体在8s内的v – t 图象；（要求计算出相应数值）
（3）在8s内水平力F所做的功。
(1)滑块A在斜面上滑下时的高度h；(2)滑块A最终与D点间的距离．
