设数列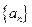 的前
的前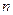 和为
和为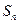 ,已知
,已知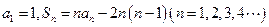
(1)设数列 的前
的前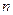 和为
和为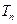 ,证明:
,证明: ;
;
(2)是否存在自然数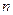 ,使得
,使得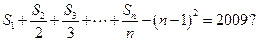 若存在,求出的值;若不存在,请说明理由。
若存在,求出的值;若不存在,请说明理由。
. 已知函数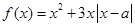 ,其中
,其中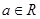 ,
,
(1)当 时,把函数
时,把函数 写成分段函数的形式;
写成分段函数的形式;
(2)当 时,求
时,求 在区间[1,3]上的最值;
在区间[1,3]上的最值;
(3)设 ,函数
,函数 在(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围
在(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围
(用 表示).
表示).
函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且
(1)确定函数的解析式;(2)证明函数 在
在 上是增函数;
上是增函数;
(3)解不等式 .
.
.已知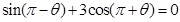 ,其中
,其中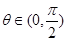
(1)求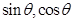 的值;
的值;
(2)求函数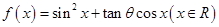 的值域.
的值域.
已知函数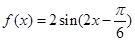

(1)用“五点法”画出函数在长度为一个周期的闭区间上的图像;
(2)求函数的单调递增区间;
(3)若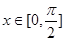 时,函数
时,函数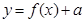 的最小值为
的最小值为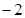 ,求实数
,求实数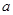 的值.
的值.
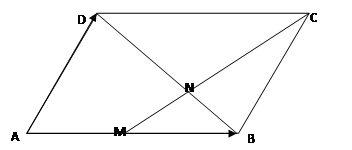
.已知平行四边形ABCD中,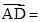
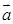 ,
,
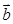 , M为AB中点,N为BD靠近B的三等分点.
, M为AB中点,N为BD靠近B的三等分点.
(1)用基底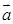 ,
,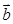 表示向量
表示向量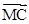 ,
,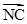 ;
;
(2)求证:M、N、C三点共线.