如图所示,P、Q为两个都带正电,并且电荷量相等的点电荷,O为它们连线的中点,A.B为它们垂直平分线上的两点,A点较近而B点较远.A.B两点的场强分别为EA和EB,电势分别为φA和φB,下面的说法中正确的是[ ]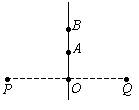
A.EA一定大于EB,φA一定高于φB
B.EA不一定大于EB,φA一定高于φB
C.EA一定大于EB,φA不一定高于φB
D.EA不一定大于EB,φA不一定高于φB
两个沿竖直方向的磁感强度大小相等、方向相反的匀强磁场穿过光滑的水平桌面,它们的宽度均为L.质量为m、边长为L的平放在桌面上的正方形线圈的ab边与磁场边界ee′的距离为L,如图所示.线圈在恒力作用下由静止开始沿桌面加速运动,ab边进入右边的磁场时恰好做速度为v的匀速直线运动.求:
(1)当ab边刚越过ff′时线圈的加速度.
(2)当ab边运动到ff′与gg′之间的正中间位置时,线圈又恰好做匀速直线运动,从ab边刚越过ee′到达右边磁场正中间位置的过程中,线圈共产生多少热量?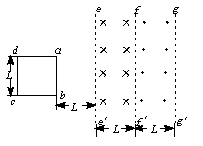
位于竖直平面内的金属框abcd,其水平边L1="1.0" m,竖直边L2="0.5" m,线框的质量m="0.2" kg,电阻R="2" Ω,在线框的下方有一上、下边界均为水平方向的匀强磁场,磁场区域宽度H>L2,磁感应强度B="1.0" T,方向与线框平面垂直,使线框的cd边从距磁场上边界高h="0.7" m处由静止开始下落.已知线框的cd边进入磁场后,ab边到达磁场上边界之前速度已达到这一阶段的最大值.求从线框下落到cd边刚刚到达磁场下边界过程中,磁场作用于线框的安培力所做的总功(g="10" m/s2,空气阻力不计).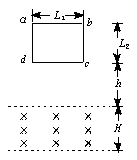
如图所示,物块A的质量为M,物块B、C的质量都是m,都可以看作质点,且m<M<2m。A与B、B与C用不可身长的轻线通过轻滑轮相连,A与地面用劲度系数为k的轻弹簧连接,物块B与物块C的距离和物块C到地面的距离相等,假设C物块落地后不反弹。若物块A距滑轮足够远,且不计一切阻力。则:
(1)若将B与C间的轻线剪断,求A下降多大距离时速度最大;
(2)若B与C间的轻线不剪断,将物块A下方的轻弹簧剪断后,要使物块B不与物块C相碰,则M与m应满足什么关系?(不计物块B、C的厚度)
2006年第九届北京国际车展,奇瑞汽车将展出中国第一辆自主品牌混合动力车奇瑞A5ISG。这是继丰田、奔驰等国际品牌后,国内自主品牌首次展出可以量产的混合动力车型。一种采用电力和汽油机双动力驱动的新型汽车,质量为m,当它在平直的公路上行驶时,若只采用汽油机驱动,发动机额定功率为P1,汽车能达到的最大速度为v1;在汽车行驶过程中由于某种原因汽车停在倾角为θ的坡道上,为了保证汽车上坡时有足够大的动力,需改为电力驱动,此时发动机的额定功率为P2.已知汽车在坡道上行驶时所受的阻力是在平直公路上行驶时的k倍,重力加速度为g,求汽车在坡道上能达到的最大速度。
如图所示,质量为3m的足够长木板C 静止在光滑水平面上,质量均为m 的两个物体A、B 放在C 的左端,A、B 间相距s0,现同时对A、B施加水平向右的瞬间冲量而使之分别获得初速度v0和2v0,若A、B与C之间的动摩擦因数分别为μ 和 2 μ ,则:
(1)最终A、B、C的共同速度为多大
(2)求A达到最小速度时,系统产生的热量Q。