某次足球赛共12支球队参加，分三个阶段进行：
（1）小组赛：经抽签分成甲、乙两组，每组6队进行单循环比赛，以积分及净剩球数取前两名；
（2）半决赛：甲组第一名与乙组第二名，乙组第一名与甲组第二名作主客场交叉淘汰赛（每两队主客场各赛一场）决出胜者;
(3)决赛：两个胜队参加决赛一场，决出胜负.
问全部赛程共需比赛多少场？
（本小题满分14分）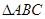
中，角A，B,C的对边分别是
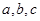且满足
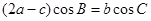
（１）求角B的大小；
（２）若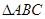的面积为为
，求
的值；
（本小题满分14分）
如图，在直三棱柱ABC-A1B1C1中，已知
，M为A1B与AB１的交点，N为棱B1C1的中点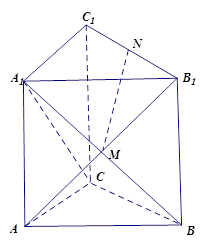
（１）求证：MN∥平面AA１C１C
（２）若AC＝AA1，求证：MN⊥平面A1BC
（本小题14分）已知函数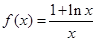
（Ⅰ）若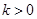
且函数
在区间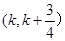
上存在极值，求实数
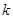的取值范围；
（Ⅱ）如果当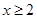
时，不等式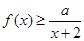
恒成立，求实数
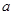的取值范围；
（Ⅲ）求证：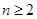
，
……
.
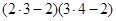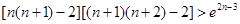（本小题13分）已知两定点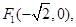
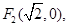满足条件
的点P的轨迹是曲线E，直线
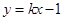与曲线E交于A、B两点。如果
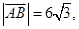且曲线E上存在点C，使
.
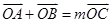（Ⅰ）求曲线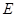
的方程；
（Ⅱ）求AB的直线方程；
（Ⅲ）求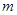
的值.
（本小题12分）已知数列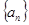
有
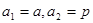（常数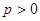
），对任意的正整数
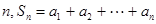，并有
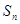满足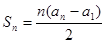
。
（Ⅰ）求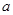
的值并证明数列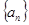为等差数列；
（Ⅱ）令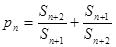
，是否存在正整数M，使不等式
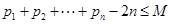恒成立，若存在，求出M的最小值，若不存在，说明理由。