在△ABC中，a＝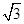
，b＝
，B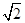＝45°.求角A、C和边c.
设函数f(x)＝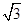
sinxcosx＋cos2x＋a.
(1)写出函数f(x)的最小正周期及单调递减区间；
(2)当x∈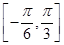
时，函数f(x)的最大值与最小值的和为
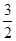，求a的值．
设函数f(x)＝(sinωx＋cosωx)2＋2cos2ωx(ω＞0)的最小正周期为
.
(1)求ω的最小正周期；
(2)若函数y＝g(x)的图象是由y＝f(x)的图象向右平移
个单位长度得到，求y＝g(x)的单调增区间．
已知ω＞0，a＝(2sinωx＋cosωx，2sinωx－cosωx)，b＝(sinωx，cosωx)．f(x)＝a·b.f(x)图象上相邻的两个对称轴的距离是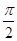
.
(1)求ω的值；
(2)求函数f(x)在区间
上的最大值和最小值．
已知函数f(x)＝sin
cos＋cos2－
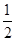
(1)若f(α)＝
，α∈(0，π)，求α的值；
(2)求函数f(x)在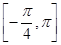
上最大值和最小值．