在一次测量万有引力常量的实验中,一个球的质量为1.2 kg,另一个球的质量是0.5 kg,两球相距10 cm,测得它们的引力是3.96×10-9 N.已知地球表面的重力加速度为9.8 m/s2,地球半径是6 400 km,根据这个数据计算地球的质量.
我国自行设计的气象同步卫星在赤道上方距离地球表面h高度处的圆轨道上绕地球运动,已知地球的自转周期为T,地球的半径为R,卫星的质量为m.
(1)用题中所给的物理量求出卫星在同步轨道上运行时的动能和受到的地球引力大小.
(2)卫星在持续运行若干年的过程中,由于长期受到微弱的阻力以及月球干扰影响,卫星的轨道高度会发生变化。因此,在同步卫星上安装了离子推进器,利用推进器的推力,可以使卫星处于指定的轨道上,若推进器在△t时间内以相对卫星的速度u向后喷出△m质量的等离子气体,以卫星为参考系,求在推进器工作时间内等离子气体所受的平均作用力大小.
如图所示,倾角为θ的光滑斜面上放有两个质量均为m的小球A和B,两球之间用一根长为L的轻杆相连,下面的小球B离斜面底端的高度为h。两球从静止开始下滑,不计球与地面碰撞时的机械能损失,且地面光滑,求: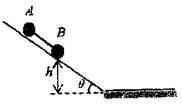
(1)两球都进入光滑水平面时两小球运动的速度大小;
(2)此过程中杆对B球所做的功。
如图11所示,在水平面上有一个质量为m的物体,在水平拉力F作用下由静止开始移动一段距离后,到达斜面底端。这时撤去外力,物体冲上斜面,沿斜面上滑的最大距离和水平面上移动的距离相等。然后物体又沿斜面滑下,并恰好停在水平面上的出发点。已知斜面倾角θ=30°,物体与水平面和斜面间的动摩擦因数相等。求物体受到的水平力F。(不考虑物体过底端时的能量损失)
如图所示,P、Q为足够长的光滑平行固定导轨,两者之间的距离为L=20cm,其电阻不计。导轨所在平面有沿竖直方向的匀强磁场,磁感应强度大小为B=5T,导轨右端连接着一电路,其中R1=10Ω,R2=20Ω,R3=15Ω,R4=25Ω,平行板电容器板间距离d="10cm" ,电容C=5μF,板间有一质量为m=1.0×10-8kg,带电量为q=-0.5×10-8 C的带电液滴。导体棒ab的电阻不计,质量为M=0.5kg,垂直于导轨PQ放置且与之良好接触,在外力作用下,ab始终沿水平方向向左做匀速直线运动。当开关S接通位置1时,带电液滴恰好处于静止状态。试回答以下问题:(重力加速度g=10m/s2)
(1)判断导轨平面内磁感线的方向,要求简要说明理由。
(2)求外力做功的功率。
(3)计算当开关由位置1转换到位置2时,带电液滴的加速度及流过电容器的电量。
如图所示,平行板电容器两板间距离为d,所带电量为Q,且上极板带正电。一质量为m,带电量为q的小球,在离平行板电容器上极板小孔A的正上方h处自由释放,到达下极板时小球的速度恰好为零(小球不与下极板接触)。已知重力加速度为g。
(1)试分析小球所带电荷的性质,并简要说明小球的运动过程。
(2)小球开始下落到速度减为零的过程中所用的时间和最大速度分别为多少?
(3)电容器的电容为多少?