如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l交于A、B两点,过A、B分别作l的垂线与圆
C过F的切线交于点P和点Q,则P、Q必在以F为焦点,l为准线的同一条抛物线上.
(Ⅰ)建立适当的坐标系,求出该抛物线的方程;
(Ⅱ)对以上结论的反向思考可以得到另一个命题:
“若过抛物线焦点F的直线与抛物线交于P、Q两点,
则以PQ为直径的圆一定与抛物线的准线l相切”请
问:此命题是否正确?试证明你的判断;
(Ⅲ)请选择椭圆或双曲线之一类比(Ⅱ)写出相应的命题并
证明其真假.(只选择一种曲线解答即可,若两种都选,则以第一选择为评分依据)
如图,设 点是圆
点是圆 上的动点,过点
上的动点,过点
 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为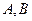 ,切线
,切线 分别交
分别交 轴于
轴于 两点.
两点.
(1)求四边形 面积的最小值;
面积的最小值;
(2)是否存在点 ,使得线段
,使得线段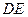 被圆
被圆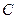 在点
在点 处的切线平分?若存在,求出点
处的切线平分?若存在,求出点 的纵坐标
的纵坐标 ;若不存在,说明理由.
;若不存在,说明理由.
如图,在平行四边形 中,
中, ,
, ,
, 为线段
为线段 的中线,将△
的中线,将△ 沿
沿 直线
直线 翻折成△
翻折成△ ,使平面
,使平面 ⊥平面
⊥平面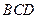 ,
,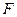 为线
为线 段
段 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)设 为线段
为线段 的中点,求直线
的中点,求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
已知一隧道的截面 是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有
是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有 米的距离,现有一货车,车宽
米的距离,现有一货车,车宽 米,车高
米,车高 米.
米.
(1)若此隧道为单向通行,经测量隧道的跨度是 米,则应如何设计隧道才能保证此货车正常通行?
米,则应如何设计隧道才能保证此货车正常通行?
(2)圆可以看作是长轴短轴相等的特殊椭圆,类比圆面积公式,
请你推测椭圆 的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
求经过点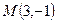 ,且与圆
,且与圆 相切于点
相切于点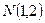 的圆
的圆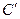 的方程,并判断两圆是外切还是内切?
的方程,并判断两圆是外切还是内切?
直线 经过点
经过点 ,且与圆
,且与圆 相交与
相交与 两点,截得的弦长为
两点,截得的弦长为 ,求
,求 的方程?
的方程?