
侧棱PA=PD= ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中
BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(1)求证:PO⊥平面ABCD;
(2)求异面直线PB与CD所成角的余弦值;
(3)线段AD上是否存在点Q,使得它到平面PCD的距离为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图所示,将一矩形花坛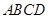 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求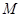 在
在 的延长线上,
的延长线上,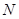 在
在 的延长线上,且对角线
的延长线上,且对角线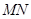 过
过 点.已知
点.已知 米,
米,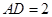 米。
米。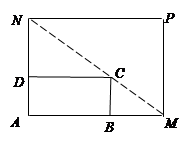
(1)设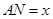 (单位:米),要使花坛
(单位:米),要使花坛 的面积大于32平方米,求
的面积大于32平方米,求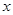 的取值范围;
的取值范围;
(2)若 (单位:米),则当
(单位:米),则当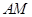 ,
,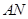 的长度分别是多少时,花坛
的长度分别是多少时,花坛 的面积最大?并求出最大面积.
的面积最大?并求出最大面积.
如图,在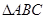 中,
中,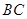 边上的中线
边上的中线 长为3,且
长为3,且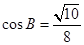 ,
, .
.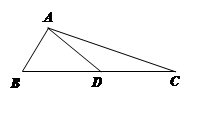
(Ⅰ)求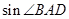 的值;(Ⅱ)求
的值;(Ⅱ)求 边的长.
边的长.
已知 ,
, .
.
(1)若 ,求
,求 的值;
的值;
(2)若 ,
, 求
求 的值.
的值.
如图,正三棱柱 中,点
中,点 是
是 的中点.
的中点.
(Ⅰ)求证:  平面
平面 ;
;
(Ⅱ)求证: 平面
平面 .
.
已知函数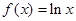 ,
, 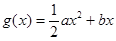
 .
.
(1)若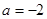 , 函数
, 函数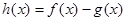 在其定义域是增函数,求
在其定义域是增函数,求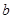 的取值范围;
的取值范围;
(2)在(1)的结论下,设函数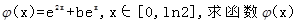 的最小值;
的最小值;
(3)设函数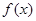 的图象
的图象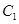 与函数
与函数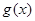 的图象
的图象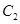 交于点
交于点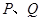 ,过线段
,过线段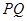 的中点
的中点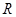 作
作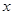 轴的垂线分别交
轴的垂线分别交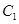 、
、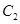 于点
于点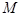 、
、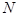 ,问是否存在点
,问是否存在点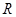 ,使
,使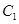 在
在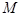 处的切线与
处的切线与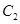 在
在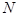 处的切线平行?若存在,求出
处的切线平行?若存在,求出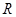 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.