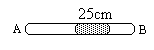
如图所示,一端封闭一端开口的粗细均匀的玻璃管横截面积为10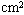 ,管内有两个自重不计的绝热活塞封闭了长30cm的气柱A及长15cm的气柱B.活塞乙用一根劲度系数k=
,管内有两个自重不计的绝热活塞封闭了长30cm的气柱A及长15cm的气柱B.活塞乙用一根劲度系数k=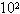 N/m、原长15cm的轻质弹簧与管底相连.气体初始温度为27℃.现在甲活塞上放一个2kg的砝码,加热气体B,保持A的温度不变,求当气体B的温度升为多少时,活塞甲可返回原处?(设大气压
N/m、原长15cm的轻质弹簧与管底相连.气体初始温度为27℃.现在甲活塞上放一个2kg的砝码,加热气体B,保持A的温度不变,求当气体B的温度升为多少时,活塞甲可返回原处?(设大气压 Pa,摩擦不计,g=10m/
Pa,摩擦不计,g=10m/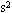 )
)
如图所示,气缸的横截面积为S,它与容器B用一个带阀门K的细管连通(细管容积不计).开始时K关闭,气缸A内充有一定质量的理想气体,B内为真空,气缸A的活塞上放有砝码,此时A内气体温度为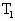 ,活塞静止时与气缸底部的距离为H,打开阀门K后,活塞下降.若将A、B内气体的温度都升高到
,活塞静止时与气缸底部的距离为H,打开阀门K后,活塞下降.若将A、B内气体的温度都升高到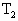 时,活塞仍可升高到原来的高度H.再让A、B内气体的温度恢复到
时,活塞仍可升高到原来的高度H.再让A、B内气体的温度恢复到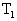 ,并将活塞上的砝码取走,这时活塞又恢复到原来的高度H.若已知大气压强为
,并将活塞上的砝码取走,这时活塞又恢复到原来的高度H.若已知大气压强为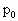 ,活塞质量为m,活塞与气缸间摩擦可忽略不计.求容器B的容积
,活塞质量为m,活塞与气缸间摩擦可忽略不计.求容器B的容积 和活塞上砝码的质量m.
和活塞上砝码的质量m.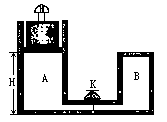
左管封闭、右管开口,内径粗细均匀的玻璃U形管竖直放置。左管内封闭一定质量的理想气体,气柱长15cm,温度为27℃,足够长的右管内用长为5cm的水银柱封闭另一质量一定的理想气体,气柱长20cm,右管置于恒温环境中。此时左管内水银面位于刻度A处且比右管内水银面高5cm(如图所示),现仅对左管内气体加热至127℃(外界大气压强p0=75cmHg。)问:
(1)为使左管内水银液面仍保持在刻度A处,则必须在右管中缓慢注入多长的水银柱?
(2)此时右管内气柱的长度是多少?
活塞面积为50 ,上放一重物,它和活塞的总质量为10kg,大气压强为1.0×
,上放一重物,它和活塞的总质量为10kg,大气压强为1.0× Pa,取g=10m/
Pa,取g=10m/ ,开始时,活塞处于静止状态,活塞和缸底距离10cm,气体温度为27℃,现给气体慢慢加热,使气体温度升高到87℃,活塞重新静止后,将活塞固定,接着再使温度下降到原来的27℃,求:活塞上升的距离?最后气体的压强?
,开始时,活塞处于静止状态,活塞和缸底距离10cm,气体温度为27℃,现给气体慢慢加热,使气体温度升高到87℃,活塞重新静止后,将活塞固定,接着再使温度下降到原来的27℃,求:活塞上升的距离?最后气体的压强?
如图所示,有一热空气气球,为了保持内外压强相等,在气球的下方开一小孔与外部空气相通.在气球的内部安装一温度调节器,通过调节气球内部空气的温度使气球上升或下降.已知气球的容积 ,(设气球内部空气温度变化时其容积保持不变),气球质量(球内空气质量不计在内)为180Kg.地面大气温度为280K,大气密度为1.2kg/
,(设气球内部空气温度变化时其容积保持不变),气球质量(球内空气质量不计在内)为180Kg.地面大气温度为280K,大气密度为1.2kg/ .那么为了使气球从地面上升,对气球内空气最低应加热到多少度?
.那么为了使气球从地面上升,对气球内空气最低应加热到多少度?
一水平放置的两端封闭、粗细均匀的玻璃管,其长度为1m.在管中有一段25cm长的水银柱将气体分为两部分A、B,它们的压强均为75cmHg,左端A气体的温度为177℃,右端B的温度为87℃,待水银柱稳定后将玻璃管放入27℃的恒温箱中,若仍使两段气体的体积不变,需使玻璃管哪端慢慢抬起,需要抬起多高?