粗细均匀的一段封闭圆柱形气缸开口向上放置，当加上一直径等于气缸内径，质量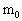
＝3kg的活塞时，封闭气体的体积变为气缸容积的9/10，此时封闭气体的温度
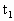＝47℃，不计活塞与气缸壁之间的摩擦，下面三种方案都可以使被封气体体积减小．
方案一：保持其它条件不变，使温度降低到
；
方案二：保持其它条件不变，在活塞上加上一个质量为m重物；
方案三：保持其它条件不变，使气缸以加速度a竖直向上做匀加速直线运动．
(1)若方案一、二使气体减小相同体积，在方案二中m＝8.4kg，则在方案一中的是多少K？
(2)若方案二、三使气体减小相同体积，写出a与m的对应关系式，并求当m＝6kg时a的大小．
在水平铁轨上放置一门质量为M的炮车，发射的炮弹质量为m，设铁轨和炮车间摩擦不计，求：（1）水平发射炮弹时，炮弹速度为v0,问：炮车的反冲速度是多大？
（2）炮身水平方向，炮弹出炮口时，相对炮口速度为v0，问：炮身的反冲速度为多大？
（3）炮车车身与水平方向成θ角，炮弹速度大小为v0，问：炮身反冲速度是多大？
如图所示，A为一具有光滑曲面的固定轨道，轨道底端是水平的，质量M=40kg的小车B静止于轨道右侧，其板面与轨道底端靠近且在同一水平面上，一个质量m=20kg的物体C以2.0m/s的初速度从轨道顶滑下，冲上小车B后经一段时间与小车相对静止并继续一起运动。若轨道顶端与底端水平面的高度差h为0.80m，物体与小车板面间的动摩擦因数μ为0.40，小车与水平面间的摩擦忽略不计，（取g=10m/s2），求：
（1）物体与小车保持相对静止时的速度；
（2）从物体冲上小车到与小车相对静止所用的时间；
（3）物体冲上小车后相对于小车板面滑动的距离。
质量为1kg的物体在倾角30º为的光滑斜面顶端由静止释放，斜面高5m，求物体从斜面顶端滑到物体的动量变化底端过程中重力的冲量为多少？物体的动量变化为多少？
如图，绝缘水平面AB上方，MN左侧存在着水平向右的匀强电场，场强为E＝500v/m,MN和PQ之间存在着方向水平垂直纸面向里的匀强磁场，且边界MN上即无电场，将质量为m1＝0.02kg，带电量为q1＝2×10-4C的表面绝缘的物块a（视作质点）自距离MN为L＝2m的A点由静止释放，物块A向右加速，并与放置在MN边界上质量为m2＝0.06kg，带电量为q2＝6×10-2C表面绝缘的物块b发生没有机械能损失的碰撞，已知二者与水平面间的动磨擦因数均为μ＝0.1，最终发现物块b沿水平面穿出边界PQ后在无场区又运动了2s后停止运动, (g=10m/s2)，不计两物块间的库仑力，据此求解下列问题
（1） 磁场的磁感应强度大小B。
（2） 物块a再次返回边界MN时的速度大小v。
如图所示，质量为M=4kg的木板放置在光滑的水平面上，其左端放置着一质量为m=2kg的滑块(视作质点)，某时刻起同时给二者施以反向的力，如图，已知F1=6N，F2=3N，
适时撤去两力，使得最终滑块刚好可到达木板右端，且二者同时停止运动，已知力F2在t2=2s时撤去，板长为S=4.5m，g=10m/s2，求
(1)力F1的作用时间t1
(2)二者之间的动磨擦因数μ
(3) t2=2s时滑块m的速度大小