总质量为M的列车以匀速率v0在平直轨道上行驶,各车厢受的阻力都是车重的k倍,而与车速无关.某时刻列车后部质量为m的车厢脱钩,而机车的牵引力不变,则脱钩的车厢刚停下的瞬间,前面列车的速度是多少?
一台理想变压器原线圈匝数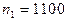 匝,两个副线圈的匝数分别是
匝,两个副线圈的匝数分别是 匝,
匝, 匝。若通过两个副线圈中的电流强度分别是
匝。若通过两个副线圈中的电流强度分别是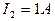 ,
,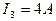 ,求原线圈中的电流强度(结果保留两位有效数字)。
,求原线圈中的电流强度(结果保留两位有效数字)。
如图所示,一辆汽车A拉着装有集装箱的拖车B,以速度v1=30 m/s进入向下倾斜的直车道。车道每100 m下降2 m。为了使汽车速度在s=200 m的距离内减到v2=10 m/s,驾驶员必须刹车。假定刹车时地面的摩擦阻力是恒力,且该力的70%作用于拖车B,30%作用于汽车A。已知A的质量m1=2000 kg,B的质量m2=6000 kg。求汽车与拖车的连接处沿运动方向的相互作用力。取重力加速度g=10 m/s2。
一质量为M,倾角为θ的楔形木块,静置在水平桌面上,与桌面间的动摩擦因数为μ,一物块质量为m,置于楔形木块的斜面上,物块与斜面的接触是光滑的。为了保持物块相对斜面静止,可用一水平力F推楔形木块,如图所示。此水平力的大小等于__________。
某人在地面上最多可举起100kg的物体,当他在以a=2m/s2的加速度匀加速上升的电梯中,最多可举起多少千克的物体?当他在以a=2m/s2的加速度匀加速度下降的电梯中,又能举起多少千克的物体?(g取10m/s2)