如图,平行四边形OABC,顶点O、A、C分别表示0,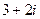 ,
,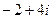 ,试求:
,试求:
(1)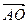 所表示的复数,
所表示的复数,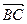 所表示的复数.
所表示的复数.
(2)对角线 所表示的复数.
所表示的复数.
(3)对角线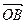 所表示的复数及
所表示的复数及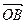 的长度.
的长度.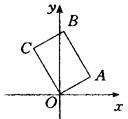
已知等差数列 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列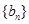 的首项为b,公比为a,其中a,b均为正整数,若
的首项为b,公比为a,其中a,b均为正整数,若 。
。
(1)求 、
、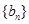 的通项公式;
的通项公式;
(2)若 成等比数列,求数列
成等比数列,求数列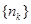 的通项公式。
的通项公式。
(3)设
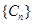 的前n项和为
的前n项和为 ,求当
,求当 最大时,n的值。
最大时,n的值。
平面内有向量 ,点
,点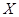 为直线OP上的一动点。
为直线OP上的一动点。
(1)当 取最小值时,求
取最小值时,求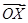 的坐标;
的坐标;
(2)当点X满足(1)的条件时求 。
。
如图,AC是一山坡,它与地面所成角为 ,B是山坡AC上一点,它和A点距离是a米,从A和B处测得山下平地D处的俯角分别是
,B是山坡AC上一点,它和A点距离是a米,从A和B处测得山下平地D处的俯角分别是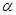 和
和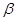 ,求C、D两点间距离。
,求C、D两点间距离。
数列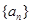 满足
满足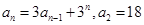
(1)证明数列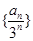 为等差数列;(2)求
为等差数列;(2)求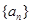 的前n项和
的前n项和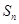 。
。
在锐角△ABC中, 分别为角A,B,C所对的边,且
分别为角A,B,C所对的边,且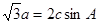 。
。
①求角C的大小。
②若C= ,且△ABC的面积为
,且△ABC的面积为 ,求
,求 的值。
的值。