设数列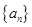 的各项均为正数.若对任意的
的各项均为正数.若对任意的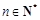 ,存在
,存在 ,使得
,使得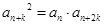 成立,则称数列
成立,则称数列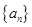 为“Jk型”数列.
为“Jk型”数列.
(1)若数列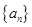 是“J2型”数列,且
是“J2型”数列,且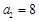 ,
, ,求
,求 ;
;
(2)若数列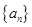 既是“J3型”数列,又是“J4型”数列,证明:数列
既是“J3型”数列,又是“J4型”数列,证明:数列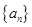 是等比数列.
是等比数列.
(理)(14分)设函数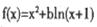 ,其中
,其中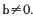
(I)当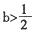 时,判断函数
时,判断函数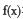 在定义域上的单调性;
在定义域上的单调性;
(II)求函数 的极值点;
的极值点;
(III)证明对任意的正整数n,不等式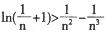 都成立.
都成立.
已知在数列 中,
中, ,
, 是其前
是其前 项和,且
项和,且
(I)求 ;(II)证明:数列
;(II)证明:数列 是等差数列;
是等差数列;
(III)令 ,记数列
,记数列 的前
的前 项和为
项和为 .求证:当
.求证:当 时,
时,  。
。
已知圆 及定点
及定点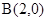 ,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足
,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足 ,
, =0.
=0.
(I)求P点所在的曲线C的方程;
(II)过点B的直线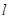 与曲线C交于M、N两点,直线
与曲线C交于M、N两点,直线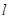 与y轴交于E点,若
与y轴交于E点,若 为定值。
为定值。
如图已知直角梯形 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
,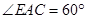 ,
, .
.
(I)在直线 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面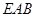 ?请证明你的结论;
?请证明你的结论;
(II)求平面 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值。
的余弦值。
高三年级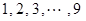 班参加高考体检,
班参加高考体检, 个班中,任选
个班中,任选 个班先参加视力检查. (I)求这
个班先参加视力检查. (I)求这 个班中恰有
个班中恰有 个班班级序号是偶数的概率;
个班班级序号是偶数的概率;
(II)设 为这
为这 个班中两班序号相邻的组数(例如:若选出的班为
个班中两班序号相邻的组数(例如:若选出的班为 班,则有两组相邻的,
班,则有两组相邻的, 班和
班和 班,此时
班,此时 的值是
的值是 ).求随机变量
).求随机变量 的分布列及其数学期望
的分布列及其数学期望 .
.