已知圆 及定点
及定点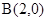 ,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足
,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足 ,
, =0.
=0.
(I)求P点所在的曲线C的方程;
(II)过点B的直线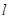 与曲线C交于M、N两点,直线
与曲线C交于M、N两点,直线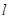 与y轴交于E点,若
与y轴交于E点,若 为定值。
为定值。
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),总成本为G(x)(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本);销售收入R(x)(万元)满足:R(x)= 假定该产品产销平衡,那么根据上述统计规律求下列问题.
假定该产品产销平衡,那么根据上述统计规律求下列问题.
(1)要使工厂有赢利,产量x应控制在什么范围内?
(2)工厂生产多少台产品时,可使赢利最多?
要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示),在窗框为定长的条件下,要使窗户能够透过最多的光线,窗户应设计成怎样的尺寸?
已知f(x)=-3x2+a(6-a)x+b.
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a、b的值.
已知不等式(2+x)(3-x)≥0的解集为A,函数f(x)= (k<0)的定义域为B.
(k<0)的定义域为B.
(1)求集合A;
(2)若集合B中仅有一个元素,试求实数k的值;
(3)若BA,试求实数k的取值范围.
已知关于x的不等式: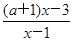 <1.
<1.
(1)当a=1时,解该不等式;
(2)当a>0时,解该不等式.