已知函数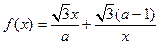 (
(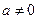 且
且 ).
).
(1) 试就实数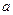 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;
(2) 已知当 时,函数在
时,函数在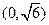 上单调递减,在
上单调递减,在 上单调递增,求
上单调递增,求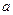 的值并写出函数的解析式;
的值并写出函数的解析式;
(3) (理)记(2)中的函数的图像为曲线 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线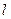 ,使得
,使得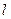 为曲线
为曲线 的对称轴?若存在,求出
的对称轴?若存在,求出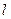 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(文) 记(2)中的函数的图像为曲线 ,试问曲线
,试问曲线 是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
(本小题满分12分)
从全校参加数学竞赛的学生的试卷中抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的小长方形的高之比为1:3:6:4:2,最右边一组的频数是6,请结合直方图提供的信息,解答下列问题:
(1)样本的容量是多少?
(2)列出频率分布表;
(3)成绩落在哪个范围内的人数最多?并求出该小组的频数,频率;
(4)估计这次竞赛中,成绩高于60分的学生占总人数的百分比.
(本小题满分12分)
已知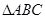 的面积
的面积 满足
满足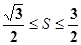 ,且
,且 ,
, 与
与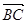 的夹角为
的夹角为 .
.
(1)求 的取值范围;
的取值范围;
(2)求函数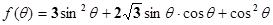 的最大值及最小值.
的最大值及最小值.
(本小题满分12分)
设 是实数,
是实数,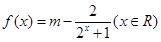 ,
,
(1)若函数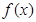 为奇函数,求
为奇函数,求 的值;
的值;
(2)试用定义证明:对于任意 ,
,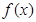 在
在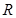 上为单调递增函数;
上为单调递增函数;
(3)若函数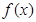 为奇函数,且不等式
为奇函数,且不等式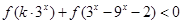 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题满分12分)已知函数
(1)若 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。
(2)求 在区间
在区间 上的最小值
上的最小值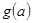 的表达式。
的表达式。
(本小题满分12分)如图是从上下底面处在水平状态下的棱长为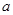 的正方体
的正方体 中分离出来的:
中分离出来的:
(1)试判断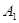 是否在平面
是否在平面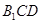 内;(回答是与否)
内;(回答是与否)
(2)求异面直线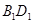 与
与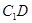 所成的角;
所成的角;
(3)如果用图示中这样一个装置来盛水,那么最多可以盛多少体积