(本小题满分12分)
从全校参加数学竞赛的学生的试卷中抽取一个样本,考察竞赛的成绩分布,将样本分成5组,绘成频率分布直方图,图中从左到右各小组的小长方形的高之比为1:3:6:4:2,最右边一组的频数是6,请结合直方图提供的信息,解答下列问题:
(1)样本的容量是多少?
(2)列出频率分布表;
(3)成绩落在哪个范围内的人数最多?并求出该小组的频数,频率;
(4)估计这次竞赛中,成绩高于60分的学生占总人数的百分比.
已知 ,且
,且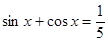
(I)求 的值;(II)求
的值;(II)求 的值.
的值.
(北京理15)已知函数 .
.
(Ⅰ)求 的最小正周期及
的最小正周期及 的对称中心:
的对称中心:
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(本小题10分)已知向量 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3), =(5-m,-(3+m)).
=(5-m,-(3+m)).
(I)若点A、B、C能构成三角形,求实数m应满足的条件;
(II)若△ABC为直角三角形,且∠A为直角,求实数m的值.
(本小题满分14分)设函数 的定义域是R,对于任意实数
的定义域是R,对于任意实数 ,恒有
,恒有 ,且当
,且当 时,
时,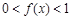 .
.
(Ⅰ)若 ,求
,求 的值;(Ⅱ)求证:
的值;(Ⅱ)求证: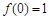 ,且当
,且当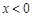 时,有
时,有 ;
;
(Ⅲ)判断 在R上的单调性,并加以证明.
在R上的单调性,并加以证明.
(本小题满分14分)已知函数 ,试证明f(x)在区间(-2,+∞)上是增函数,并求出该函数在区间[1,4]上的最大值和最小值.
,试证明f(x)在区间(-2,+∞)上是增函数,并求出该函数在区间[1,4]上的最大值和最小值.