设函数f(x)=x2+(lga+2)x+lgb,g(x)=2x+2,若f(-1)=0,且对一切实数x,不等式f(x)≥g(x)恒成立;
(Ⅰ)(本问5分)求实数a、b的值;
(Ⅱ)(本问7分)设F(x)=f(x)-g(x),数列{an}满足关系an=F(n),
证明: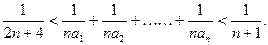
如图,在三棱柱 中,已知
中,已知
 ,
, 侧面
侧面
(1)求直线C1B与底面ABC所成角的正弦值;
(2)在棱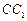 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得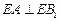 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若 ,求二面角
,求二面角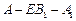 的大小.
的大小.
(本小题满分12分)
某计算机程序每运行一次都随机出现一个二进制的六位数 ,其中
,其中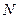 的各位数中,
的各位数中, ,
, (
( 2,3,4,5)出现0的概率为
2,3,4,5)出现0的概率为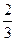 ,出现1的概率为
,出现1的概率为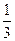 ,记
,记 ,当该计算机程序运行一次时,求随机变量X的分布列和数学期望.
,当该计算机程序运行一次时,求随机变量X的分布列和数学期望.
(本小题满分12分)
已知集合 ,
,
①当 时,求
时,求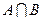
②求使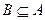 的实数
的实数 的取值范围。
的取值范围。
函数 的定义域为
的定义域为 ,且满足对任意
,且满足对任意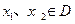 ,
,
有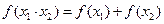
(1)求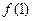 的值;
的值;
(2)判断 的奇偶性并证明你的结论;
的奇偶性并证明你的结论;
(3)如果 ,
, ,且
,且 在
在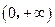 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
某渔业公司年初用98万元购买一艘捕鱼船,第一年各种费用12 万元,以后每年都增加4万元,每年捕鱼收益50万元.
万元,以后每年都增加4万元,每年捕鱼收益50万元.
(1)问第几年开始获利;
(2)若干年后,有两种处理方案:①年平均获利最大时,以26万元出售该渔船;②总纯收入获利最大时,以8万元出售该渔船.问哪种方案最合算.