以椭圆
+y2=1(a>1)短轴的一个端点B(0,1)为直角顶点作椭圆的内接等腰直角三角形,问这样的直角三角形是否存在?如果存在,请说明理由,并判断最多能作出几个这样的三角形;如果不存在,请说明理由.
（本小题满分14分）已知在四棱锥P-ABCD中，底面ABCD是边长为4的正方形，△PAD是正三角形，平面PAD⊥平面ABCD，E、F、G分别是PA、PB、BC的中点．
（I）求证：EF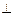
平面PAD；
（II）求平面EFG与平面ABCD所成锐二面角的大小；
（本小题满分14分）一袋子中有大小、质量均相同的10个小球，其中标记“开”字的小球有5个，标记“心”字的小球有3个，标记“乐”字的小球有2个．从中任意摸出1个球确定标记后放回袋中，再从中任取1个球．不断重复以上操作，最多取3次，并规定若取出“乐”字球，则停止摸球．求：
（Ⅰ）恰好摸到2个“心”字球的概率；
（Ⅱ）摸球次数
的概率分布列和数学期望．
(本题满分14分) 在△ABC中, 角A, B, C所对的边分别为a, b, c, 且满足
.
(Ⅰ) 求
的值;
(Ⅱ) 若△ABC的面积是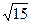
, 求
的值.
（本小题满分12分）
某公司生产一种电子仪器的固定成本为20000元，每生产一台仪器需增加投入100元，已知总收益满足函数：
其中
是仪器的月产量.
（1）将利润表示为月产量的函数
；
（2）当月产量为何值时，公司所获得利润最大？最大利润是多少？
（本小题满分14分）
已知函数
且
，
（1）求
的值；
（2）判定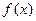
的奇偶性；
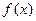（3）判断在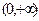
上的单调性，并给予证明．