(本小题满分15分)某生产旅游纪念品的工厂,拟在2010年度将进行系列促销活动.经市场调查和测算,该纪念品的年销售量x万件与年促销费用t万元之间满足3-x与t+1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2010年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为:“年平均每件生产成本的150%”与“年平均每 件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)(1)求出x与t所满足的关系式;(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
写出集合B={x|0<x<4,x∈N}的所有真子集.
已知二次函数 .
.
(1)设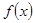 在
在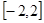 上的最大值、最小值分别是
上的最大值、最小值分别是 、
、 ,集合
,集合 ,且
,且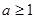 ,记
,记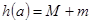 ,求
,求 的最小值.
的最小值.
(2)当 时,
时,
①设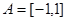 ,不等式
,不等式 的解集为C,且
的解集为C,且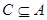 ,求实数
,求实数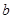 的取值范围;
的取值范围;
②设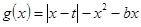
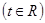 ,求
,求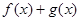 的最小值.
的最小值.
已知函数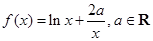 .
.
(1)若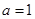 ,求函数
,求函数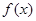 的极值;
的极值;
(2)若函数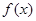 在
在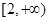 上是增函数,求实数
上是增函数,求实数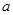 的取值范围;
的取值范围;
(3)若函数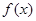 在
在 上的最小值为3,求实数
上的最小值为3,求实数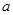 的值.
的值.
海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为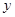 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里 处,如图,现假设:①失事船的移动路径可视为抛物线
处,如图,现假设:①失事船的移动路径可视为抛物线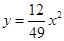 ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为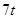

(1)当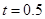 时,写出失事船所在位置
时,写出失事船所在位置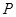 的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)
的纵坐标,若此时两船恰好会合,求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角,用符号及其满足的条件表示即可)
(2)问救援船的时速至少是多少海里才能追上失事船?
设数列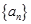 的前n项和为
的前n项和为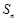 ,且满足
,且满足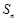 =2-
=2- ,
,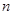 =1,2,3,….
=1,2,3,….
(1)求数列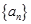 的通项公式;
的通项公式;
(2)若数列 满足
满足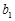 =1,且
=1,且 =
= +
+ ,求数列
,求数列 的通项公式;
的通项公式;
(3)设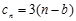 ,求数列
,求数列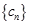 的前
的前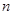 项和为
项和为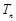 .
.