海事救援船对一艘失事船进行定位：以失事船的当前位置为原点，以正北方向为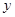
轴正方向建立平面直角坐标系（以1海里为单位长度），则救援船恰好在失事船正南方向12海里
处，如图，现假设：①失事船的移动路径可视为抛物线
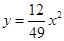；②定位后救援船即刻沿直线匀速前往救援；③救援船出发
小时后，失事船所在位置的横坐标为
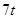
（1）当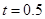
时，写出失事船所在位置
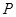的纵坐标，若此时两船恰好会合，求救援船速度的大小和方向 (若确定方向时涉及到的角为非特殊角，用符号及其满足的条件表示即可)
（2）问救援船的时速至少是多少海里才能追上失事船？
已知圆M:x2+y2-2mx-2ny+m2-1=0与圆N:x2+y2+2x+2y-2=0交于A、B两点，且这两点平分圆N的圆周 ，求圆M的半径最小时的圆M的方程.
已知定点A(0,1)，B(0,－1)，C(1,0).动点P满足：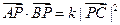
.
(1)求动点P的轨迹方程，并说明方程表示的曲线；
(2)当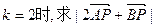
的最大值和最小值.
某厂拟生产甲、乙两种适销产品，每件利润分别为300、500元，甲、乙产品的部件各自在A、B两个车间分别生产，每件甲、乙产品的部件分别需要A、B车间的生产能力1、2工时；两种产品的部件最后都要在C车间装配，装配每件甲、乙产品分别需要3、4工时.A、B、C三个车间每天可用于生产这两种产品的工时分别为8、12、36，应如何安排生产这两种产品才能获利最多？
设直线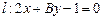
的倾斜角为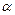
.
（1）若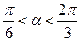
，试求B的取值范围；
（2）若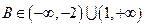
，求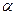
的取值范围.
已知圆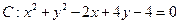
，问是否存在斜率为1的直线
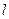，使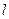被圆C截得弦AB，以AB为直径的圆经过原点，若存在，写出直线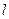的方程；若不存在，说明理由.