试在下面的简单情况下,由牛顿定律推导动能定理:质点在斜向上与水平方向成α角的恒力F和阻力f作用下,沿水平方向做匀加速直线运动.
如图15-5-8所示,带负电的粒子垂直磁场方向进入圆形匀强磁场区域,出磁场时速度偏离原方向60°角.已知带电粒子质量m=3×10-20kg,电荷量q=10-13C,速度v0=105m/S,磁场区域的半径R= ×10-1m,不计重力.求磁场的磁感应强度.
×10-1m,不计重力.求磁场的磁感应强度.

图15-5-8 图15-5-9
图15-5-15是测量带电粒子质量的仪器工作原理示意图,设法使某有机化合物的气态分子导入图中所示的容器A中,使它受到电子束轰击,失去一个电子变成为正一价的分子离子,分子离子从狭缝S1以很小的速度进入电压为U的加速电场区(初速度不计),加速后,再通过狭缝S2、S3射入磁感应强度为B的匀强磁场,方向垂直于磁场区的界面PQ.最后,分子离子打到感光片上,形成垂直于纸面且平行狭缝S3的细线.若测得细线到狭缝S3的距离为d.导出分子离子的质量m的表达式.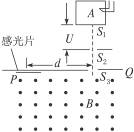
图15-5-15
如图所示,一个电子从M板附近由静止开始被电场加速,又从N板的小孔水平射出,并垂直磁场方向进入一个半径为R的圆形匀强磁场B的区域.若入射点为b,且v0与Ob成30°角,要使电子在磁场中飞过的距离最大,则两板间的电势差U是多大?(电子质量为m、电荷量为e)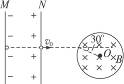
如图15-5-10所示,匀强磁场的磁感应强度为B,垂直纸面向里,宽度为d 0,一电荷量为e的电子以水平速度v 0垂直射入磁场中,穿出磁场时,速度与竖直方向的夹角为60°.求:
(1)电子的质量m;
(2)电子在磁场中的运动时间.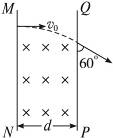
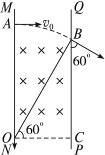
图15-5-10 图15-5-11
如图所示,水平放置的厚度均匀的铝箔,置于匀强磁场中,磁场方向垂直纸面向里,一带电粒子进入磁场后在磁场中做匀速圆周运动,到达P点垂直穿过铝箔后仍做匀速圆周运动,粒子每次穿过铝箔时损失的能量都相同,如图中两圆弧半径R=25 cm,r="20" cm.问:
(1)这个粒子带何种电荷;
(2)该粒子总共能穿过铝箔多少次?