已知甲、乙、丙等6人 .
（1）这6人同时参加一项活动，必须有人去，去几人自行决定，共有多少种不同的去法？
（2）这6人同时参加6项不同的活动，每项活动限1人参加，其中甲不参加第一项活动，乙不参加第三项活动，共有多少种不同的安排方法？
（3）这6人同时参加4项不同的活动，求每项活动至少有1人参加的概率.
如图，已知抛物线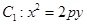
的焦点在抛物线
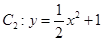上．
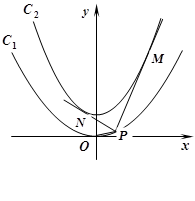
（Ⅰ）求抛物线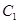
的方程及其准线方程；
（Ⅱ）过抛物线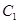上的动点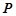
作抛物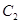线
的两条切线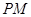
、
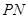， 切点为
、
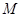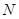．若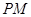、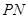的斜率乘积为
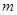，且
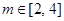，求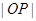
的取值范围．
已知函数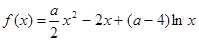
，
．
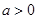（Ⅰ）若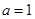
，求函数
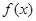的极值；
（Ⅱ）若函数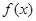在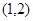
上有极值，求
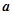的取值范围．
如图，在四棱锥P-ABCD中，PA⊥平面ABCD， AB//CD，∠DAB=90°，PA=AD=DC=1，AB=2，M为PB的中点．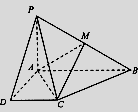
（I）证明：MC//平面PAD；
（II）求直线MC与平面PAC所成角的余弦值．
已知数列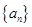
中，
，
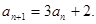
（Ⅰ）记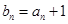
，求证：数列
为等比数列；
（Ⅱ）求数列
的前
项和