两个相同的小球，分别挂在不能伸长的线上，两线互相平行，两个小球的重心位于同一水平线上。而且两球相互接触。第一个球摆线长
=1m，第二个球摆线长
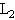=0.25m，把第二个球提到一个很小的角度后释放，它在4s内和第一个球共碰撞了多少次?（设碰撞时间很短，可以忽略，碰撞能量不损失，g=9.86m/
）
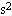（1）小车的水平长度和磁场的宽度
（2）小车的位移
时线圈中的电流大小
以及此时小车的加速度
（3）在线圈进入磁场的过程中通过线圈某一截面的电量
（4）线圈和小车通过磁场的过程中线圈电阻的发热量
如图所示，质量为1kg的物体静置于水平面上，现对物体施以水平方向的恒定拉力，1s末将拉力撤去，物体运动的
图象如图所示，试求：
（1）滑动摩擦力的大小；
（2）拉力的大小；
（3）在0~3s内滑动摩擦力做的功。
宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引力作用，设每个星体的质量均为m，四颗星稳定地分布在边长为a的正方形的四个顶点上，已知这四颗星均围绕正方形对角线的交点做匀速圆周运动，引力常量为G，试求：
（1）求星体做匀速圆周运动的轨道半径；
（2）若实验观测得到星体的半径为R，求星体表面的重力加速度；
（3）求星体做匀速圆周运动的周期．
右图是一个设计“过山车”的试验装置的工作原理示意图，光滑斜面与竖直平面内的圆形轨道的最低点B平滑连接，圆形轨道半径为R，一质量为m的小车(可视为质点)在A点由静止释放并沿斜面滑下，当小车第一次经过B点进入圆形轨道时对轨道B点的压力为其所受重力的7倍，小车恰能越过圆形轨道最高点C完成圆周运动并第二次经过最低点B再沿水平轨道向右运动。已知重力加速度的大小为g。
(1)求A点距水平面的高度h；
(2)假设小车在竖直圆轨道的左、右半圆轨道部分克服摩擦阻力做功相等，求小车第二次经过 圆轨道最低点B时速度有多大?
如图，匀强电场的方向水平向右。一个质量为m，电荷量为+q的小球，以初速度v0从a点竖直向上射入电场中，小球通过电场中的b点时速度为2v0，方向恰好水平向右，求：
（1）a、b两点间的距离
。
（2）a、b两点间的电势差
。