(本小题13分)如图,在直三棱柱ABC-A1B1C1中, ,点E、F、G分别是AA1、
,点E、F、G分别是AA1、
AC、BB1的中点,且CG⊥C1G .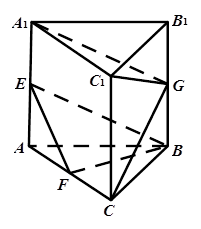
(1)求证:CG//面BEF;
(2)求证:面BEF⊥面A1C1G .
(本小题13分)已知命题A:方程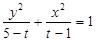 表示焦点在
表示焦点在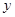 轴上的椭圆;
轴上的椭圆;
命题B:实数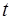 使得不等式
使得不等式 成立。
成立。
(1)若命题A为真,求实数 的取值范围;
的取值范围;
(2)若命题B是命题A的必要不充分条件,求实数 的取值范围。
的取值范围。
(本小题13分)已知双曲线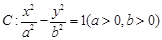 的离心率为
的离心率为 ,实轴长为2。
,实轴长为2。
(1)求双曲线C的方程;
(2)若直线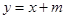 被双曲线C截得的弦长为
被双曲线C截得的弦长为 ,求
,求 的值。
的值。
(本小题满分14分)在平面直角坐标系 中,已知圆
中,已知圆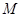 过坐标原点O且圆心在曲线
过坐标原点O且圆心在曲线 上.
上.
(Ⅰ)若圆M分别与 轴、
轴、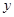 轴交于点
轴交于点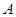 、
、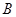 (不同于原点O),求证:
(不同于原点O),求证: 的面积为定值;
的面积为定值;
(Ⅱ)设直线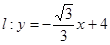 与圆M 交于不同的两点C,D,且
与圆M 交于不同的两点C,D,且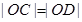 ,求圆M的方程;
,求圆M的方程;
(Ⅲ)设直线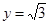 与(Ⅱ)中所求圆M交于点
与(Ⅱ)中所求圆M交于点 、
、 ,
,  为直线
为直线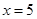 上的动点,直线
上的动点,直线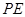 ,
,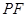 与圆M的另一个交点分别为
与圆M的另一个交点分别为 ,
, ,求证:直线
,求证:直线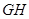 过定点.
过定点.
(本小题满分13分)已知关于 的二次函数
的二次函数
(Ⅰ)设集合 和
和 ,分别从集合
,分别从集合 ,
,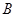 中随机取一个数作为
中随机取一个数作为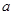 和
和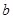 ,求函数
,求函数 在区间
在区间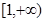 上是增函数的概率.
上是增函数的概率.
(Ⅱ)设点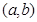 是区域
是区域 内的随机点,求函数
内的随机点,求函数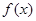 在区间
在区间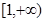 上是增函数的概率.
上是增函数的概率.