在大风的情况下,一小球自A点竖直上抛,其运动轨迹如图所示,(小球的运动可看作竖直方向的竖直上抛运动和水平方向的初速度为零的匀加速直线运动的合运动),小球运动轨迹上A、B两点在同一水平直线上,M点为轨迹的最高点,若风力的大小恒定,方向水平向右,小球抛出时的动能为4J,在M点时它的动能为2J,不计其它阻力,求:
(1)小球水平位移S1与S2的比值
(2)小球所受风力F与重力G的比值(结果可用根式表示)
(3)小球落回B点时的动能
质量为m的小球B用一根轻质弹簧连接.现把它们放置在竖直固定的内壁光滑的直圆筒内,平衡时弹簧的压缩量为 ,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于
,如图所示,小球A从小球B的正上方距离为3x0的P处自由落下,落在小球B上立刻与小球B粘连在一起向下运动,它们到达最低点后又向上运动,并恰能回到0点(设两个小球直径相等,且远小于 略小于直圆筒内径),已知弹簧的弹性势能为
略小于直圆筒内径),已知弹簧的弹性势能为 ,其中k为弹簧的劲度系数,Δx为弹簧的形变量。求:
,其中k为弹簧的劲度系数,Δx为弹簧的形变量。求:
(1)小球A质量。
(2)小球A与小球B一起向下运动时速度的最大值.

质量为M的小车静止在光滑的水平面上,小车的上表面是一光滑的曲面,末端是水平的,如下图所示,小车被挡板P挡住,质量为优的物体从距地面高H处自由下落,然后沿光滑的曲面继续下滑,物体落地点与小车右端相距 ,若撤去挡板P,物体仍从原处自由落下,求物体落地时落地点距离小车右端多远?
,若撤去挡板P,物体仍从原处自由落下,求物体落地时落地点距离小车右端多远?
中国首个月球探测计划“嫦娥工程”将分三个阶段实施:首先在2007年发射环绕月球的卫星“嫦娥一号”,深入了解月球;到2012年发射月球探测器,在月球上进行实地探测;到2017年送机器人上月球,建立观测站,实地实验采样并返回地球,为载人登月及月球基地选址做准备。设想我国宇航员随“嫦娥”号登月飞船登陆月球,在飞船贴近月球表面时可近似看成绕月球做匀速圆周运动,飞船上备有以下实验仪器:
| A.计时表一只, | B.弹簧秤一把, | C.已知质量为 的物体一个, 的物体一个, |
D.天平一只(附砝码一盒)。宇航员测量出飞船在靠近月球表面的圆形轨道绕行 圈所用的时间为 圈所用的时间为 ,飞船在月球上着陆后,宇航员利用所带的仪器又进行了第二次测量,并利用测量结果计算出了月球的半径和质量。若已知万有引力常量为G,则: ,飞船在月球上着陆后,宇航员利用所带的仪器又进行了第二次测量,并利用测量结果计算出了月球的半径和质量。若已知万有引力常量为G,则: |
(1)说明宇航员是如何进行第二次测量的?
(2)利用宇航员测量的量(用符号表示)来求月球的半径和质量。

在车厢顶上吊有一单摆,摆长为L,如下图所示,当小车向左运动时,悬线偏向竖直方向的左边一个恒定的角度,使这个单摆摆动,摆动的平面与小车的前进方向在同一平面内,测得振动周期为T,求放在该车厢地板上质量为M的物体在相对车厢静止时受到的摩擦力的大小和方向。
如下图所示,两面平行的玻璃砖下表面涂有反射物质,一束与上表面成30°入射的光线,在右端垂直标尺上形成了A、B两个光斑,A、B间距为4cm,已知玻璃砖的折射率为 ,面出形成两光斑的光路网,并求此玻璃砖的厚度
,面出形成两光斑的光路网,并求此玻璃砖的厚度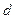 。
。