(本小题满分14分)
某化妆品生产企业为了占有更多的市场份额,拟在2005年度进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销费t万元之间满足3-x与t+1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件。已知2005年生产化妆品的设备折旧和维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%与“平均每件促销费的一半”之和,则当年生产的化妆品正好能销完.
⑴将2005年的利润y(万元)表示为促销费t(万元)的函数;
⑵该企业2005年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入—生产成本—促销费,生产成本=固定费用+生产费用)
如图,在三棱锥 中,已知△
中,已知△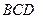 是正三角形,
是正三角形, 平面
平面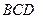 ,
,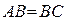 ,
,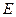 为
为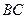 的中点,
的中点, 在棱
在棱 上,且
上,且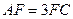 ,
,
(1)求证: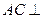 平面
平面 ;
;
(2)求平面 与平面
与平面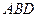 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
(3)若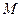 为
为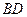 的中点,问
的中点,问 上是否存在一点
上是否存在一点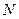 ,使
,使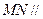 平面
平面 ?若存在,说明点
?若存在,说明点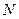 的位置;若不存在,试说明理由.
的位置;若不存在,试说明理由.
如图,矩形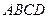 与正三角形
与正三角形 中,
中,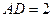 ,
,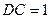 ,
,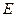 为
为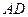 的中点。现将正三角形
的中点。现将正三角形 沿
沿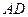 折起,得到四棱锥的三视图如下:
折起,得到四棱锥的三视图如下:
(1)求四棱锥 的体积;
的体积;
(2)求异面直线 所成角的大小。
所成角的大小。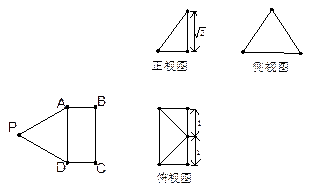
已知直线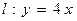 和点
和点 ,点
,点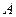 为第一象限内的点且在直线
为第一象限内的点且在直线 上,直线
上,直线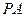 交
交 轴正半轴于点
轴正半轴于点 ,求△
,求△ 面积的最小值,并求当△
面积的最小值,并求当△ 面积取最小值时的
面积取最小值时的 的坐标。
的坐标。
已知直线 过两直线
过两直线 和
和 的交点,且直线
的交点,且直线 与点
与点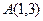 和点
和点 的距离相等,求直线
的距离相等,求直线 的方程。
的方程。
(本小题满分15分)
记函数 .
.
(1)若函数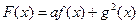 在
在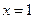 处取得极值,试求
处取得极值,试求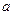 的值;
的值;
(2)若函数 有两个极值点
有两个极值点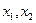 ,
,
且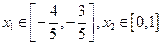 ,试求
,试求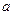 的取值范围;
的取值范围;
(3)若函数 对任意
对任意 恒有
恒有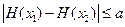 成立,试求
成立,试求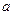 的取值范围.(参考:
的取值范围.(参考: )
)