已知椭圆 ,
,
(1)求斜率为2的平行弦的中点轨迹方程。
(2)过A(2,1)的直线L与椭圆相交,求L被截得的弦的中点轨迹方程;
(3)过点P(0.5,0.5)且被P点平分的弦所在直线的方程。
已知函数 ,其中
,其中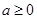 。
。
(1)若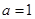 ,求函数
,求函数 的极值点和极值;
的极值点和极值;
(2)求函数 在区间
在区间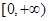 上的最小值。
上的最小值。
已知数列 中,
中, ,其中
,其中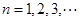 。
。
(1)计算 的值;
的值;
(2)根据计算结果猜想 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。
已知数列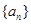 满足:
满足: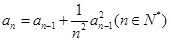
(1)若数列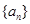 是以常数
是以常数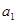 为首项,公差也为
为首项,公差也为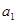 的等差数列,求
的等差数列,求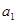 的值;
的值;
(2)若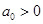 ,求证:
,求证: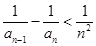 对任意
对任意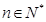 都成立;
都成立;
(3)若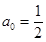 ,求证:
,求证: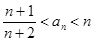 对任意
对任意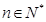 都成立;
都成立;
已知圆M: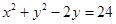 ,直线
,直线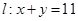 ,
,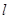 上一点A的横坐标为
上一点A的横坐标为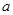 ,过点A作圆M的两条切线
,过点A作圆M的两条切线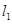 ,
,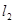 ,切点分别为B,C.
,切点分别为B,C.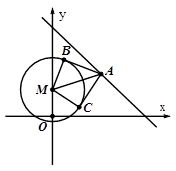
(1)当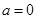 时,求直线
时,求直线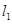 ,
,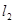 的方程;
的方程;
(2)当直线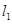 ,
,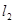 互相垂直时,求
互相垂直时,求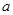 的值;
的值;
(3)是否存在点A,使得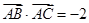 ?若存在,求出点A的坐标,若不存在,请说明理由.
?若存在,求出点A的坐标,若不存在,请说明理由.
已知函数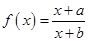 (
(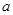 、
、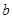 为常数).
为常数).
(1)若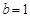 ,解不等式
,解不等式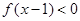 ;
;
(2)若 ,当
,当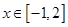 时,
时,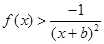 恒成立,求
恒成立,求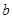 的取值范围.
的取值范围.