如图,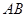 是⊙
是⊙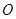 的直径,
的直径, 是弦,
是弦,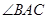 的平分线
的平分线 交⊙
交⊙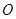 于点
于点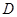 ,
, ,交
,交 的延长线于点
的延长线于点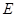 ,
,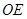 交
交 于点
于点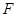 .
.
(1)求证: 是⊙
是⊙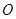 的切线;
的切线;
(2)若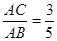 ,求
,求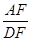 的值
的值
如图,圆 的半径OB垂直于直径AC,M为AO上一点,BM的延长线交
的半径OB垂直于直径AC,M为AO上一点,BM的延长线交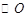 于N,过N点的切线交CA的延长线于P.
于N,过N点的切线交CA的延长线于P.
(1)求证: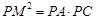 ;
;
(2)若圆 的半径为
的半径为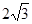 ,
,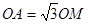 ,求MN的长 .
,求MN的长 .
已知函数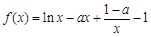 (
(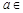
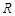 )
)
(1)当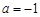 时,求曲线
时,求曲线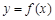 在
在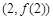 处的切线方程;
处的切线方程;
(2)当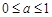 时,试讨论
时,试讨论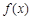 的单调性.
的单调性.
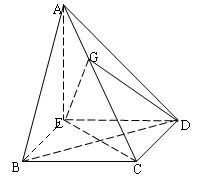
如图,在四棱锥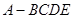 中,
中,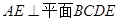 ,
,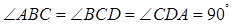 ,
,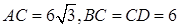 .
.
(1)求证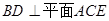 ;
;
(2)设点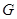 在棱
在棱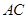 上,且
上,且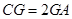 ,试求三棱锥E—GCD的体积.
,试求三棱锥E—GCD的体积.
已知数列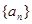 的前
的前 项和为
项和为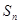 ,且
,且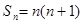 ,
,
(1)求数列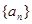 的通项公式
的通项公式
(2)数列 的通项公式
的通项公式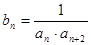 ,求数列
,求数列 的前
的前 项和为
项和为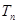
已知函数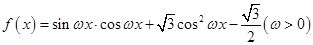 ,直线
,直线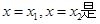
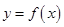 图象的任意两条对称轴,且
图象的任意两条对称轴,且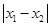 的最小值为
的最小值为 .
.
(1)求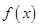 在
在 的单调增区间;
的单调增区间;
(2)将函数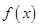 的图象向右平移
的图象向右平移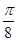 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数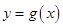 的图象,若关于
的图象,若关于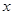 的方程
的方程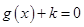 ,在区间
,在区间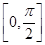 上有解,求实数k的取值范围.
上有解,求实数k的取值范围.