已知函数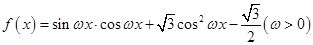 ,直线
,直线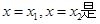
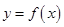 图象的任意两条对称轴,且
图象的任意两条对称轴,且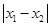 的最小值为
的最小值为 .
.
(1)求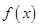 在
在 的单调增区间;
的单调增区间;
(2)将函数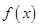 的图象向右平移
的图象向右平移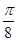 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数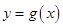 的图象,若关于
的图象,若关于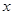 的方程
的方程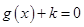 ,在区间
,在区间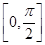 上有解,求实数k的取值范围.
上有解,求实数k的取值范围.
若圆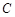 经过坐标原点和点
经过坐标原点和点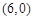 ,且与直线
,且与直线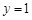 相切, 从圆
相切, 从圆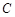 外一点
外一点 向该圆引切线
向该圆引切线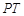 ,
, 为切点,
为切点,
(Ⅰ)求圆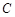 的方程;
的方程;
(Ⅱ)已知点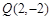 ,且
,且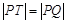 , 试判断点
, 试判断点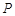 是否总在某一定直线
是否总在某一定直线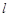 上,若是,求出
上,若是,求出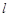 的方程;若不是,请说明理由;
的方程;若不是,请说明理由;
(Ⅲ)若(Ⅱ)中直线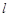 与
与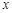 轴的交点为
轴的交点为 ,点
,点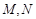 是直线
是直线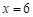 上两动点,且以
上两动点,且以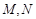 为直径的圆
为直径的圆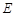 过点
过点 ,圆
,圆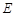 是否过定点?证明你的结论.
是否过定点?证明你的结论.
已知⊙M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切⊙M于A,B两点.
(Ⅰ)若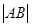 =
=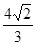 ,求
,求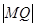 及直线MQ的方程;
及直线MQ的方程;
(Ⅱ)求证:直线AB恒过定点.
三角形ABC的三个顶点A(1,3)B(1,﹣3)C(3,3),求
(Ⅰ)BC边上中线AD所在直线的方程;
(Ⅱ)三角形ABC的外接圆O1的方程;
(Ⅲ)已知圆O2: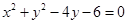 ,求圆心在x-y-4=0,且过圆O1与圆O2交点的圆的方程。
,求圆心在x-y-4=0,且过圆O1与圆O2交点的圆的方程。
如图,棱锥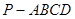 的底面
的底面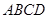 是矩形,
是矩形,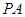 ⊥平面
⊥平面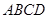 ,
, .
.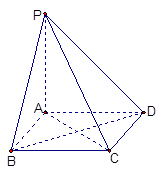
(1)求证:BD⊥平面PAC;
(2)求二面角P—CD—B的大小;
(3)求点C到平面PBD的距离.
如图是一个正三棱柱(以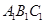 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为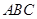 .已知
.已知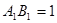 ,
,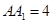 ,
,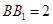 ,
,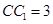 .
.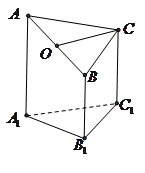
(1)设点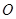 是
是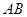 的中点,证明:
的中点,证明: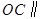 平面
平面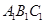 ;
;
(2)求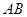 与平面
与平面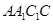 所成的角的正弦值;
所成的角的正弦值;