甲、乙两人各射击一次,击中目标的概率分别是 .假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ.
.假设两人射击是否击中目标,相互之间没有影响; 每人各次射击是否击中目标,相互之间也没有影响. (1)求甲射击4次,至少1次未击中目标的概率;(2)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少? (3)若甲连续射击5次,用ξ表示甲击中目标的次数,求ξ的数学期望Eξ.
已知等差数列{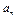 }前
}前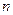 项和为
项和为 ,且
,且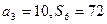
(1)求数列{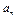 }的通项公式
}的通项公式
(2)若 ,求数列
,求数列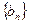 的前
的前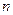 项和
项和
已知函数f(x)=xm+ax的导函数f′(x)=2x+1, ,点An(n, Sn)在函数y="f(x)" (n∈N*)的图像上 ,
,点An(n, Sn)在函数y="f(x)" (n∈N*)的图像上 ,
(1)求证:数列 为等差数列;
为等差数列;
(2)设 ,求数列
,求数列 的前
的前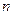 项和
项和
已知抛物线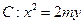
 和直线
和直线 没有公共点(其中
没有公共点(其中 、
、 为常数),动点
为常数),动点 是直线
是直线 上的任意一点,过
上的任意一点,过 点引抛物线
点引抛物线 的两条切线,切点分别为
的两条切线,切点分别为 、
、 ,且直线
,且直线 恒过点
恒过点 .
.
(1)求抛物线 的方程;
的方程;
(2)已知 点为原点,连结
点为原点,连结 交抛物线
交抛物线 于
于 、
、 两点,
两点,
证明:
已知函数 .
.
(1)当 且
且 ,
, 时,试用含
时,试用含 的式子表示
的式子表示 ,并讨论
,并讨论 的单调区间;
的单调区间;
(2)若 有零点,
有零点,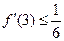 ,且对函数定义域内一切满足
,且对函数定义域内一切满足 的实数
的实数 有
有 .
.
①求 的表达式;
的表达式;
②当 时,求函数
时,求函数 的图象与函数
的图象与函数 的图象的交点坐标
的图象的交点坐标
如图, 是圆
是圆 的直径,点
的直径,点 在圆
在圆 上,
上, ,
,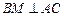 交
交 于点
于点 ,
, 平面
平面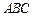 ,
, ,
, .
.
(1)证明: ;
;
(2)求平面 与平面
与平面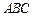 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.