已知数列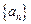 满足
满足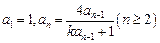 .
.
(1)求数列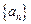 的通项公式;
的通项公式;
(2)当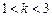 时,证明不等式:
时,证明不等式: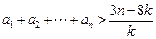 .
.
已知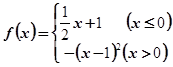
(1)求函数的最大值;(2)求使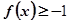 成立的x的取值范围.
成立的x的取值范围.
设函数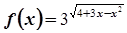
(1)求函数的定义域;
(2)求函数的值域;
(3)求函数的单调区间.
(本小题14分)已知点(1, )是函数
)是函数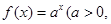 且
且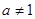 )的图象上一点,
)的图象上一点,
等比数列 的前
的前 项和为
项和为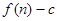 ,数列
,数列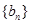
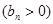 的首项为
的首项为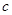 ,且前
,且前 项和
项和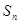 满足
满足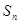 -
-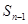 =
=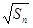 +
+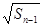 (
(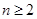 ).
).
(1)求数列 和
和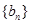 的通项公式;
的通项公式;
(2)若数列{ 前
前 项和为
项和为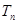 ,问
,问 的最小正整数
的最小正整数 是多少?
是多少?
(3)设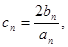 求数列
求数列 的前
的前 项和
项和
(本小题14分)在数列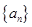 中,
中, ,
,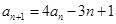 ,
, .
.
(Ⅰ)证明数列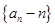 是等比数列;
是等比数列;
(Ⅱ)求数列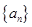 的前
的前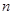 项和
项和 ;
;
(Ⅲ)证明不等式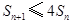 ,对任意
,对任意 皆成立.
皆成立.
(本小题14分)某公司计划在今年内同时出售变频空调机和智能洗衣机,由于这两种产品的市场需求量非常大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大已知对这两种产品有直接限制的因素是资金和劳动力,通过调查,得到关于这两种产品的有关数据如下表:
| 资金 |
单位产品所需资金(百元) |
月资金供应量(百元) |
|
| 空调机 |
洗衣机 |
||
| 成本 |
30 |
20 |
300 |
| 劳动力(工资) |
5 |
10 |
110 |
| 单位利润 |
6 |
8 |
试问:怎样确定两种货物的月供应量,才能使总利润达到最大,最大利润是多少?