(本小题14分)在数列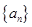 中,
中, ,
,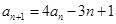 ,
, .
.
(Ⅰ)证明数列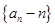 是等比数列;
是等比数列;
(Ⅱ)求数列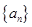 的前
的前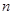 项和
项和 ;
;
(Ⅲ)证明不等式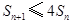 ,对任意
,对任意 皆成立.
皆成立.
如图,四棱锥P﹣ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)若PA=2,试问在线段EF上是否存在点Q,使得二面角Q﹣AP﹣D的余弦值为 ?若存在,确定点Q的位置;若不存在,请说明理由.
?若存在,确定点Q的位置;若不存在,请说明理由.
为调查市民对汽车品牌的认可度,在秋季车展上,从有意购车的500名市民中,随机抽样100名市民,按年龄情况进行统计的频率分布表Ⅰ和频率分布直方图2,
频率分布表Ⅰ

(1)频率分布表中的①②位置应填什么数?并补全频率分布直方图,再根据频率分布直方图统计这500名志愿者得平均年龄;
(2)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加的宣传活动,再从这20名中选取2名志愿者担任主要发言人.记这2名志愿者中“年龄低于30岁”的人数为X,求X的分布列及数学期望.
已知△ABC的面积为2,且满足 ,设
,设 和
和 的夹角为θ.
的夹角为θ.
(1)求 的取值范围;
的取值范围;
(2)求函数 的取值范围.
的取值范围.
设a为实数,函数 ,
, .
.
(1)求 的单调区间及极值;
的单调区间及极值;
(2)求证:当 且
且 时,
时, .
.
有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次,根据年龄将大众评委分为5组,各组的人数如下:
(Ⅰ)为了调查评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从B组中抽取了6人.请将其余各组抽取的人数填入下表.
抽取人数 6
(Ⅰ)在(Ⅰ)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.