一袋中装有分别标记着1、2、3、4 数字的4个球, 从这只袋中每次取出1个球, 取出后放回, 连续取三次, 设三次取出的球中数字最大的数为ξ.(1) 求ξ=3时的概率; (2) 求ξ的概率分布列及数学期望.
(本小题满分14分)设函数 R
R ,且
,且 为
为 的极值点.
的极值点.
(1)当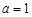 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)若 恰有两解,试求实数
恰有两解,试求实数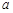 的取值范围;
的取值范围;
(3)在(1)的条件下,设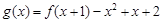 ,证明:
,证明: .
.
(本小题满分14分)已知函数 ,设曲线
,设曲线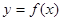 过点
过点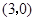 ,且在点
,且在点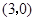 处的切线的斜率等于
处的切线的斜率等于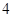 ,
,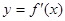 为
为 的导函数,满足
的导函数,满足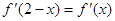 .
.
(1)求 ;
;
(2)设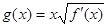 ,
,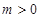 ,求函数
,求函数 在
在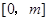 上的最大值;
上的最大值;
(3)设 ,若
,若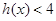 对
对 恒成立,求实数
恒成立,求实数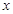 的取值范围.
的取值范围.
(本小题满分14分)已知数列 的首项
的首项 ,其前
,其前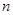 和为
和为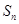 ,且满足
,且满足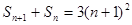 (
( N*).
N*).
(1)用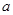 表示
表示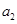 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)对任意的 N*,
N*,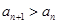 ,求实数
,求实数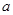 的取值范围.
的取值范围.
(本小题满分14分)已知函数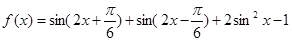 .
.
(1)求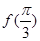 的值;
的值;
(2)求函数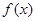 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(3)说明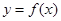 的图像是如何由函数
的图像是如何由函数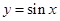 的图像变换所得.
的图像变换所得.
(本小题满分12分)已知正项等比数列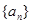 中,
中,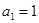 ,且
,且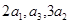 成等差数列.
成等差数列.
(1)求数列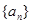 的通项公式;
的通项公式;
(2)设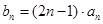 ,求数列
,求数列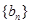 的前n项和
的前n项和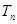 .
.