已知双曲线 的离心率e=2,A,B为双曲线上两点,线段AB的垂直平分线为
的离心率e=2,A,B为双曲线上两点,线段AB的垂直平分线为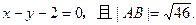
①求双曲线C经过二、四象限的渐近线的倾斜角
②试判断在椭圆C的长轴上是否存在一定点N(a,0),
使椭圆上的动点M满足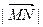 的最小值为3,若存
的最小值为3,若存
在求出所有可能的a值,若不存在说明理由.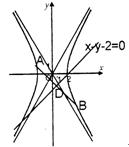
(本小题满分12分)如图,长方体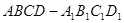 中,
中,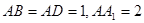 ,点
,点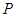 为棱
为棱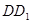 上一点.
上一点.
(1)求证:平面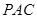 ⊥平面
⊥平面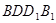 ;
;
(2)若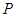 是棱
是棱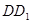 的中点,求
的中点,求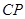 与平面
与平面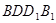 所成的角大小.
所成的角大小.
已知函数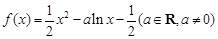 .
.
(Ⅰ)当 时,求曲线
时,求曲线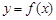 在点
在点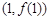 处的切线方程;
处的切线方程;
(Ⅱ)求函数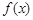 的单调区间;
的单调区间;
(Ⅲ)若对任意的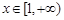 ,都有
,都有 成立,求a的取值范围.
成立,求a的取值范围.
某厂生产产品x件的总成本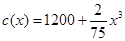 (万元),已知产品单价P(万元)与产品件数x满足:
(万元),已知产品单价P(万元)与产品件数x满足: ,生产100件这样的产品单价为50万元.
,生产100件这样的产品单价为50万元.
(1)设产量为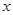 件时,总利润为
件时,总利润为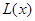 (万元),求
(万元),求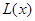 的解析式;
的解析式;
(2)产量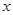 定为多少件时总利润
定为多少件时总利润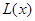 (万元)最大?并求最大值(精确到1万元).
(万元)最大?并求最大值(精确到1万元).
观察下列不等式 ,
, ,
,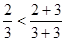 ,
,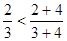 ,
,
照此规律,写出第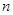 个不等式,然后判断这个不等式是否成立并给出证明.
个不等式,然后判断这个不等式是否成立并给出证明.
设函数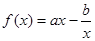 ,曲线
,曲线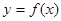 在点
在点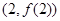 处的切线方程为7x-4y-12=0
处的切线方程为7x-4y-12=0
求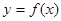 的解析式和
的解析式和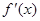 .
.