已知椭圆
的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线
是抛物线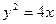
的一条切线．
（Ⅰ）求椭圆的方程；
（Ⅱ）过点
的动直线L交椭圆C于A、B两点.问：是否存在一个定点T，使得以AB为直径的圆恒过点T ? 若存在，求点T坐标；若不存在，说明理由．
（本小题满分14分）已知椭圆
的一个焦点是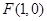
，且离心率为
.
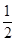（Ⅰ）求椭圆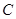
的方程；
（Ⅱ）设经过点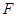
的直线交椭圆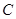于
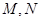两点，线段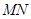
的垂直平分线交
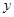轴于点
，求
的取值范围.
（本小题满分13分）已知函数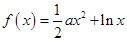
，其中
.
（Ⅰ）求
的单调区间；
（Ⅱ）若在
上的最大值是-1，求A的值.
（本小题满分14分）如图，正三棱柱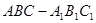
的侧棱长和底面边长均为
，
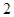是
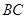的中点．
（Ⅰ）求证：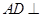
平面
；
（Ⅱ）求证：
∥平面
；
（Ⅲ）求三棱锥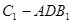
的体积．
（本小题满分13分）某种零件按质量标准分为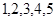
五个等级.现从一批该零件中随机抽取
个，对其等级进行统计分析，得到频率分布表如下：
| 等级 |
 |
 |
 |
 |
 |
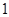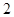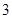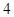| 频率 |
 |
 |
 |
 |
 |
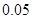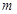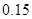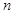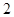（Ⅰ）在抽取的个零件中，等级为的恰有个，求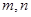
；
（Ⅱ）在（Ⅰ）的条件下，从等级为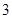和的所有零件中，任意抽取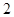个，求抽取的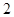个零
件等级恰好相同的概率.
（本小题满分13分）已知函数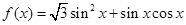
，
.
（Ⅰ）求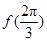
的值；
（Ⅱ）求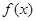
的最大值和最小值.