对于函数 。
。
(1)若 在
在 处取得极值,且
处取得极值,且 的图像上每一点的切线的斜率均不超过
的图像上每一点的切线的斜率均不超过 试求实数
试求实数 的取值范围;
的取值范围;
(2)若 为实数集R上的单调函数,设点P的坐标为
为实数集R上的单调函数,设点P的坐标为 ,试求出点P的轨迹所形成的图形的面积S。
,试求出点P的轨迹所形成的图形的面积S。
已知函数f(x)=2x,g(x)= +2.
+2.
(1)求函数g(x)的值域;
(2)求满足方程f(x)-g(x)=0的x的值.
已知函数y=2-x2+ax+1在区间(-∞,3)内递增,求a的取值范围.
对于函数f(x)若存在x0∈R,f(x0)=x0成立,则称x0为f(x)的不动点.已知f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A,B两点的横坐标是函数f(x)的不动点,且A,B两点关于直线y=kx+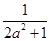 对称,求b的最小值.
对称,求b的最小值.
已知函数f(x)的图象与函数h(x)=x+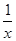 +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+ ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
已知函数f(x)=xm-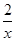 且f(4)=
且f(4)= .
.
(1)求m的值;
(2)判定f(x)的奇偶性;
(3)判断f(x)在(0,+∞)上的单调性,并给予证明.