已知椭圆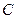 的中心在原点,一个焦点
的中心在原点,一个焦点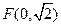 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是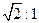 .
.
(Ⅰ)求椭圆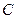 的方程;
的方程;
(Ⅱ)若椭圆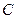 在第一象限的一点
在第一象限的一点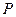 的横坐标为
的横坐标为 ,过点
,过点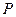 作倾斜角互补的两条不同的直线
作倾斜角互补的两条不同的直线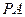 ,
,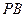 分别交椭圆
分别交椭圆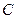 于另外两点
于另外两点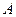 ,
,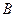 ,求证:直线
,求证:直线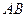 的斜率为定值;
的斜率为定值;
(Ⅲ)求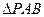 面积的最大值.
面积的最大值.
如图是总体的一个样本频率分布直方图,且在区间[15,18)内的频数为8.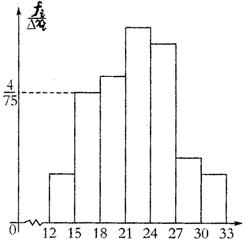
(1)求样本容量;
(2)若在[12,15)内的小矩形的面积为0.06,
①求样本在[12,15)内的频数;
②求样本在[18,33)内的频率。
集合A=(―∞,―2]∪[3,+∞),关于x的不等式(x-2a)·(x+a)>0的解集为B(其中a<0).
(1)求集合B;
(2)设p:x∈A,q:x∈B,且Øp是Øq的充分不必要条件,求a的取值范围。
已知定点A(-2,0)和B(2,0),曲线E上任一点P满足|PA|-|PB|=2.
(1)求曲线E的方程;
(2)延长PB与曲线E交于另一点Q,求|PQ|的最小值;
(3)若直线l的方程为x=a(a≤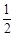 ),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。
),延长PB与曲线E交于另一点Q,如果存在某一位置,使得从PQ的中点R向l作垂线,垂足为C,满足PC⊥QC,求a的取值范围。
如图,椭圆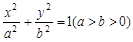 过点P(1,
过点P(1, 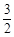 ),其左、右焦点分别为F1,F2,离心率e=
),其左、右焦点分别为F1,F2,离心率e=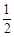 ,M,N是直线x=4上的两个动点,且
,M,N是直线x=4上的两个动点,且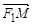 ·
·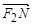 =0.
=0.
(1)求椭圆的方程;
(2)求|MN|的最小值;
(3)以MN为直径的圆C是否过定点?请证明你的结论。
如图,在四棱锥O—ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点。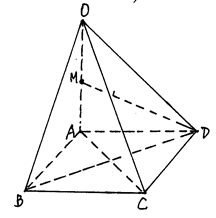
(1)求证:直线BD⊥平面OAC;
(2)求直线MD与平面OAC所成角的大小;
(3)求点A到平面OBD的距离。