已知定点A(－2,0)和B(2,0)，曲线E上任一点P满足|PA|－|PB|＝2.
（1）求曲线E的方程；
（2）延长PB与曲线E交于另一点Q，求|PQ|的最小值；
（3）若直线l的方程为x＝a(a≤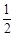
)，延长PB与曲线E交于另一点Q，如果存在某一位置，使得从PQ的中点R向l作垂线，垂足为C，满足PC⊥QC，求a的取值范围。
在2008年北京奥运会羽毛球女单决赛中，中国运动员张宁以2：1力克排名世界第一的队友谢杏芳，蝉联奥运会女单冠军.羽毛球比赛按“三局二胜制”的规则进行（即先胜两局的选手获胜，比赛结束），且各局之间互不影响.根据两人以往的交战成绩分析，谢杏芳在前两局的比赛中每局获胜的概率是0.6，但张宁在前二局战成1：1的情况下，在第三局中凭借过硬的心理素质，获胜的概率为0.6.若张宁与谢杏芳下次在比赛上相遇.
（1）求张宁以2：1获胜的概率；
（2）求张宁失利的概率.
已知函数
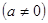是奇函数，并且函数
的图像经过点（1，3），求：（1）求实数
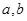的值；（2）求函数的值域
已知函数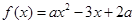
（1）若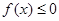
的解集为
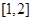，求实数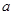
的取值范围;
（2）在(1)的条件下,求函数f(x)在区间[0,3]的值域.
已知函数
，其中
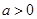
若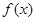
在x=1处取得极值，求a的值； 
求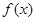的单调区间；
（Ⅲ）若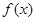的最小值为1，求a的取值范围.
有标号为1，2，3，4，5的五个红球和标号为1，2的两个白球，将这七个球排成一排，使两端都是红球.
①如果每个白球两边都是红球，共有多少种不同的排法？
②如果1号红球和1号白球相邻排在一起，共有多少种不同的排法？
③同时满足条件①②的排法有多少种？