(本小题满分12分)已知F1、F2是椭圆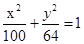 的两个焦点,P是椭圆上任意一点.
的两个焦点,P是椭圆上任意一点.
(1)若∠F1PF2=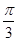 ,求△F1PF2的面积;
,求△F1PF2的面积;
(2)求PF1·PF2的最大值.
本小题满分12分)
设函数 在
在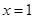 及
及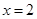 时取得极值.
时取得极值.
(Ⅰ)求a、b的值(6分);
(Ⅱ)若对于任意的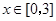 ,都有
,都有 成立,求c的取值范围(6分)
成立,求c的取值范围(6分)
(本小题满分12分)已知函数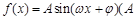 >0,
>0, >0,
>0,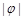 <
<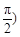 的图象与
的图象与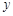 轴的交点为(0,1),它在
轴的交点为(0,1),它在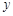 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为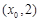 和
和
(1)写出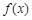 的解析式及
的解析式及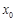 的值;
的值;
(2)若锐角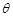 满足
满足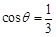 ,求
,求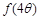 的值.
的值.
(本小题满分12分)
在一次数学考试中,第21题和第22题为选做题. 规定每位考生必须且只须在其中选做一题. 设4名考生选做每一道题的概率均为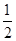 .
.
(1)求其中甲、乙两名学生选做同一道题的概率;
(2)设这4名考生中选做第22题的学生个数为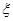 ,求
,求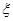 的概率分布及数学期望. 的解析
的概率分布及数学期望. 的解析
.已知关于x的一元二次方程x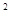 -2(a-2)x-b
-2(a-2)x-b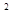 +16=0.
+16=0.
(1)若a、b是一枚骰子先后投掷两次所得到的点数,求方程有两个正实数根的概率;
(2)若a∈[2,6],b∈[0,4],求一元二次方程没有实数根的概率
已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)从中一次取2个不同的球,试列出所有基本事件;并求至少有一个是红球概率。
(3)从中取2次,每次取1个球,在放回的条件下求至少有一个是红球概率。