已知抛物线 ,直线
,直线 与C交于A,B两点,O为坐标原点。
与C交于A,B两点,O为坐标原点。
(1)当 ,且直线
,且直线 过抛物线C的焦点时,求
过抛物线C的焦点时,求 的值;
的值;
(2)当直线OA,OB的倾斜角之和为45°时,求 ,
, 之间满足的关系式,并证明直线
之间满足的关系式,并证明直线 过定点。
过定点。
(本小题满分12分)已知 <
<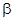 <
<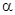 <
<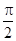 ,
,
(Ⅰ)求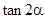 的值.
的值.
(Ⅱ)求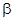 .
.
(本小题满分12分)某广场有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为 ,经测量
,经测量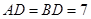 米,
米,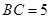 米,
米,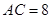 米,
米,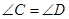 .
.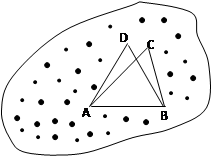
(Ⅰ)求 的长度;
的长度;
(Ⅱ)若环境标志的底座每平方米造价为5000元,不考虑其他因素,小李、小王谁的设计使建造费用较低(请说明理由)?较低造价为多少?(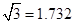 )
)
(本小题满分12分)设函数 .
.
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)若 ,求函数
,求函数 的最大值和最小值.
的最大值和最小值.
(本小题满分12分)等比数列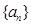 中,已知
中,已知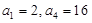
(Ⅰ)求数列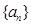 的通项公式
的通项公式
(Ⅱ)若 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 的通项公式及前
的通项公式及前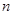 项和
项和
(本小题满分12分)已知
(1)求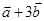 的坐标;
的坐标;
(2)当 为何实数时,
为何实数时,

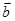 与
与 平行, 平行时它们是同向还是反向?
平行, 平行时它们是同向还是反向?